Question

How can I convert the bond-line structure of $2 - methylhexane$ to a Newman projection viewed along the ${C_3} - {C_4}$ bond?

Answer 1

We have to see the straight line structure of $2 - methylhexane$ in the structure, we can represent the structure in four forms, Sawhorse Newman Fisher and Flying structure. The Newman representation among the four has the circle diagram in which the two carbon are arranged as we are seeing the two circles.

Complete step-by-step answer:
Let’s take the $2 - methylhexane$ and firstly write it in the straight chain structure.
$C{H_3} - CH(C{H_3}) - C{H_2} - C{H_2} - C{H_2} - C{H_3}\,\,\,\,\,\,(2 - methylhexane)$
We can number them and can write them as shown in figure.

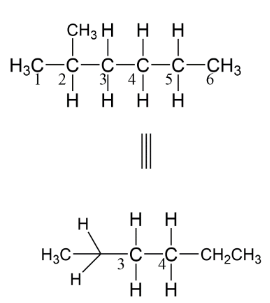
Here, as we see that $C3$ has two hydrogens and one molecule of isopropane thus we can make a circle with three bonds on which these bonds can be attached. Similarly, we have a $C4$ carbon atom having two hydrogens and one ethyl group. Now if we want to change the structure as Newman representation let’s make a circle which represents the $C4$ atom while the $C3$ represents using a dot. It means it is having such representation.

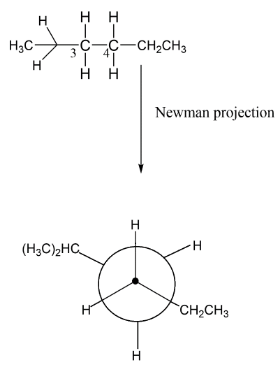
Here, the carbon atoms take their positions as you are seeing in the above figure. So, we can convert normal straight line structure into Newman projection by taking the first atom of carbon as a dot and the second is represented via a circle. The bonds are formed such that the angle between two bulky groups should be ${180^ \circ }$ so as to minimize the repulsion between the groups.

Note: It was seen in the Newman projection we can easily see the tensed state and relaxed state of the molecule. In the tensed state we have repulsion between two bulky groups as there are ethyl and isopropyl groups. So, in this state there is an angle of ${60^ \circ }$ while in a relaxed state we see that the two bulky groups are having ${180^ \circ }$ angle.