Solveeit Logo
Login

Question

Question: How can a definite integral be negative? \[\]...

How can a definite integral be negative? $$$$

Explanation

Solution

We recall the definition of definite integral of function f(x)f\left( x \right) with respect to xx within the interval [a,b]\left[ a,b \right] as the area bounded by the curve and the lines x=a,x=bx=a,x=b. We recall that area will obtained as negative if all parts of bounded region lie below x−x-axis or more parts of the region lie below x−x-axis then above x−x-axis.$$$$

Complete step-by-step answer:
We know that integral or primitive function of f(x)f\left( x \right) is given as F(x)+cF\left( x \right)+c whereddxF(x)=f(x)\dfrac{d}{dx}F\left( x \right)=f\left( x \right). If we integrate within a certain interval x∈[a,b]x\in \left[ a,b \right] rather than all over the domain then we call it a definite integral and we express it as
∫abf(x)=[F(x)]ab=F(b)−F(a)\int_{a}^{b}{f\left( x \right)}=\left[ F\left( x \right) \right]_{a}^{b}=F\left( b \right)-F\left( a \right)
The definite integral of the function f(x)f\left( x \right) is the area of the enclosed region by the curve within the area boundsx=a,x=bx=a,x=b. If all of the enclosed region lie above the x−x-axis then area as well as definite integral will be positive which means
∫abf(x)≥0 if f(x)≥0 for x∈[a,b]\int_{a}^{b}{f\left( x \right)}\ge 0\text{ if }f\left( x \right)\ge 0\text{ for }x\in \left[ a,b \right]
We can take an example f(x)=xf\left( x \right)=\sqrt{x} which is positive for the defined domain x∈(0,∞)x\in \left( 0,\infty \right). $$$$

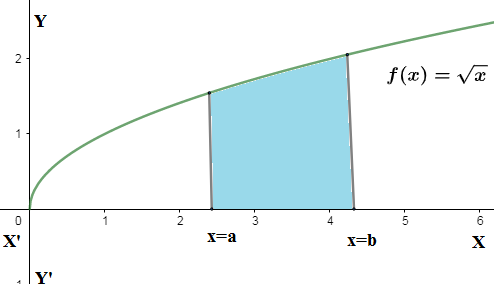
If all of the enclosed region lies blow the x−x-axis then area as well as definite integral will be negative which means
∫abf(x)≤0 if f(x)≤0 for x∈[a,b]\int_{a}^{b}{f\left( x \right)}\le 0\text{ if }f\left( x \right)\le 0\text{ for }x\in \left[ a,b \right]
We can take an example f(x)=−xf\left( x \right)=-\sqrt{x} which is negative for the defined domain x∈(0,∞)x\in \left( 0,\infty \right). $$$$

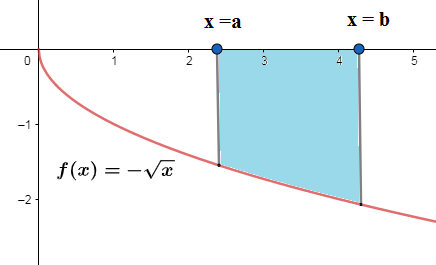
If the area of the enclosed region that lies below the x−x-axis is more than the area above the x−x-axis then the definite integral will be negative. If the curve intersects at some x=c∈[a,b]x=c\in \left[ a,b \right] then we assume the area above as Aa=∫acf(x){{A}_{a}}=\int_{a}^{c}{f\left( x \right)} and area below Ab=∫cbf(x){{A}_{b}}=\int_{c}^{b}{f\left( x \right)}. Then we have
∫abf(x)=∫acf(x)+∫cbf(x)=Aa+Ab≤0 if ∣Aa∣≤∣Ab∣\int_{a}^{b}{f\left( x \right)}=\int_{a}^{c}{f\left( x \right)}+\int_{c}^{b}{f\left( x \right)}={{A}_{a}}+{{A}_{b}}\le 0\text{ if }\left| {{A}_{a}} \right|\le \left| {{A}_{b}} \right|
Let us consider f(x)=sin⁡x,a=−π,b=−π2f\left( x \right)=\sin x,a=-\pi ,b=\dfrac{-\pi }{2} as an example. We can represent ∫−π−−π2f(x)<0\int_{-\pi }^{-\dfrac{-\pi }{2}}{f\left( x \right)}<0 as the area shaded below. $$$$

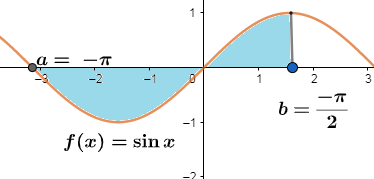
Note: We note that the definite integration of x=f(y)x=f\left( y \right)within interval y∈[a,b]y\in \left[ a,b \right]with respect to yy will be negative if the enclosed region by the curve f(y)f\left( y \right) and the bounds y=a,y=by=a,y=b will be at the left side of y−y-axis or the area at the left side will be more than area at the right side. We can find a definite integral of functions whose indefinite integral cannot be determined with approximation.