Question

How are corresponding angles of similar figures related?

Answer 1

To solve these types of questions we need to draw two triangles with particular ratio sides. Also, we need to know how to find a ratio between two measures. This question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. Also, we need to know how to compare the sides of one triangle with the side of another triangle.

Complete step by step solution:
In this question, we would find the relation between the corresponding angles of a similar figure. For that, we can make the following two figures.


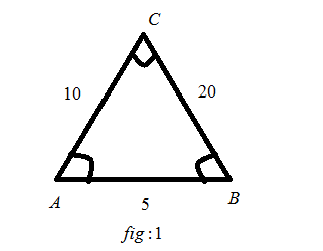
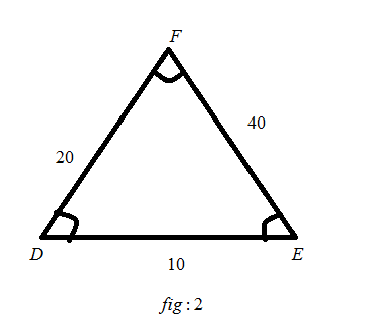
In fig: $1$, we have the length of $AB$a side is equal to $5$, the length of $BC$a side is equal to $20$, the length of $CA$ a side is equal to $10$. And $\angle A$, $\angle B$ and $\angle C$ is not mentioned. In this figure$2$, we have the length of $DE$a side is $10$, the length of $EF$ a side is $40$, and the length of $FD$ is $20$. And $\angle D$ ,$\angle E$, and $\angle F$ is not mentioned.
We know that, if the size of two triangles are in the same ratio, that is their sides are in the same ratio, then the corresponding angle of the triangle would be equal. So, let’s check the above- mentioned two figures have the same ratio.
Let’s compare the corresponding angles in the two triangles,

1. $AB$is corresponding to the$DE$
2. $BC$is corresponding to the$EF$
3. $CA$is corresponding to the$FD$
   1. $AB$is corresponding to the$DE$:

$$AB = 5 \\\ DE = 10 \\\$$

So, we get
$ratio = \dfrac{{AB}}{{DE}} = \dfrac{5}{{10}} = \dfrac{1}{2}$
2. $BC$is corresponding to the$EF$:

$$BC = 20 \\\ EF = 40 \\\$$

So, we get
$ratio = \dfrac{{BC}}{{EF}} = \dfrac{{20}}{{40}} = \dfrac{1}{2}$
3. $CA$is corresponding to the$FD$:

$$CA = 10 \\\ FD = 20 \\\$$

So, we get
$ratio = \dfrac{{CA}}{{FD}} = \dfrac{{10}}{{20}} = \dfrac{1}{2}$
So, the ratio between two triangle sides is $1:2$. So, we know that, if the three sides of a triangle are in the same ratio, then the corresponding angle will be the same.
So, we get

$$\angle A = \angle D \\\ \angle C = \angle F \\\ \angle B = \angle E \\\$$

So, the final answer is
The corresponding angles are the same in similar figures.

Note: In this type of question we would involve the arithmetic operation of addition/ subtraction/ multiplication/ division. We would remember how to find the ratio between two measures. Note that, when all the three sides of the triangle are in the same ratio then the corresponding angles are the same.