Question

Here, AB is a vertically suspended elastic cord of negligible mass and length L. Its force constant is $k=\dfrac{4mg}{L}$. There is a massless platform attached to the lower end of the cord. A monkey of mass m starts from top-end A and slides down the cord with uniform acceleration $\dfrac{g}{2}$. Just before landing on the platform, the monkey loses grip on the cord. After landing on the platform the monkey stays on it. Calculate the maximum extension in the elastic cord is

Answer 1

When any kind of mass attached to the string which has its one end fixed to a point experiences an external force the string and the mass undergo SHM (simple harmonic motion). During the successively changing harmonics, the total energy of the system always remains the same; it can just convert into the kinetic and the potential energy.
As per the given data,
Force constant of the string is $k=\dfrac{4mg}{L}$,
Acceleration of the monkey is $\dfrac{g}{2}$

Complete answer:
According to the monkey, it is moving from the string which is attached to a point. The objective of the question can be visualized clearing from the following diagram.

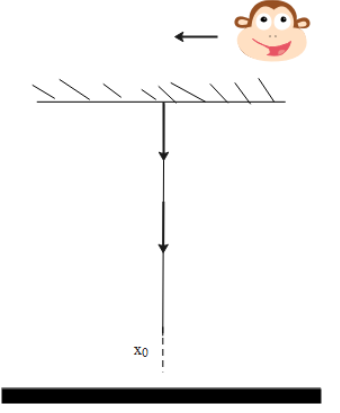
The force acting on the initiative when the monkey started to down is given as,
$F=k{{x}_{0}}\quad ...(1)$
As the monkey is moving downwards the force applied by the monkey will be,
$\begin{aligned} & F=m(g-\dfrac{g}{2}) \\\ & \Rightarrow F=m\dfrac{g}{2}\quad .....\left( 2 \right) \\\ \end{aligned}$
By putting the value of the $k$ in extension (1) and combining equation (2) and (1),
$\begin{aligned} & m\dfrac{g}{2}={{x}_{0}}\left( \dfrac{4mg}{L} \right) \\\ & \Rightarrow {{x}_{0}}=\dfrac{L}{8} \\\ \end{aligned}$
The potential energy store by the system in the starting is
$U=\dfrac{1}{2}k{{x}_{0}}$
By putting the values of the
$\begin{aligned} & U=\dfrac{1}{2}k\dfrac{4mg}{L}{{\left( \dfrac{L}{8} \right)}^{2}} \\\ & \Rightarrow U=\dfrac{mgL}{32}\quad ....(3) \\\ \end{aligned}$
The kinetic energy of the moving monkey will be given as,
${{K}_{0}}=\dfrac{1}{2}m{{v}^{2}}$
The velocity of the free-falling body is given by,
$\begin{aligned} & v=\sqrt{2gh} \\\ & So,\,{{v}^{2}}=2gh \\\ \end{aligned}$
The total distance the monkey has to cover after the first extension of the string will is,
$\begin{aligned} & h=L+\dfrac{L}{8} \\\ & \Rightarrow h=\dfrac{9L}{8} \\\ \end{aligned}$
So, the kinetic energy of the monkey is given as
${{K}_{0}}=\dfrac{9}{16}mgL\quad ....(4)$
If the cord undergo further extension the balanced energy equation will be given as,
$\begin{aligned} & {{K}_{total}}={{U}_{total}} \\\ & \Rightarrow {{K}_{0}}+mgx=\dfrac{1}{2}{{\left( kx+{{x}_{0}} \right)}^{2}}-\dfrac{1}{2}kx_{0}^{2} \\\ \end{aligned}$
By putting the values from the equation (1), (2), (3), and (4) and simplifying it we obtain a quadratic equation,
$32{{x}^{2}}-8Lx-9{{L}^{2}}=0$
So, at the roots of this quadratic equation, the value of the extension is obtained as,
$x=\dfrac{L}{8}+\dfrac{\sqrt{19}}{8}$
Thus the required answer to the question is, $\dfrac{L}{8}+\dfrac{\sqrt{19}}{8}$

Note:
Every object which is at a height from the ground has some potential energy and experiences a gravitational pull towards the ground. When the object moves from the height towards the ground it obeys the law of conservation of energy. According to this law, the total energy of a system always remains constant.