Question

Here A, B and C are three points on a circle with center O such that $\angle BOC = {30^ \circ }$ and $\angle AOB = {60^ \circ }$. If D is a point on the circle other than the arc ABC, find the value of $\angle ADC$.
(A) ${90^ \circ }$
(B) ${40^ \circ }$
(C) ${45^ \circ }$
(D) ${110^ \circ }$

Answer 1

In this question to find the value of the angle we use the theorem of the circle which states that an angle subtended by an arc of the circle at the center is double the angle is subtended at any point on the remaining circle of the same arc. Hence we find the value of the angle made at the center first and then we find the value of the angle made in the remaining part of the circle.

Complete step-by-step answer:

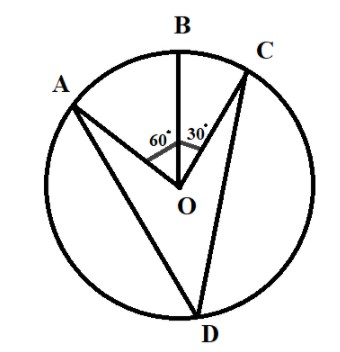
According to the question it is given that $\angle AOB = {60^ \circ }$, $\angle BOC = {30^ \circ }$
So, the value of $\angle AOC$, we get
$\therefore \angle AOC = \angle AOB + \angle BOC$
Now we put the value of $\angle AOB$, $\angle BOC$ in the above equation,
$\therefore \angle AOC = {60^ \circ } + {30^ \circ }$
Hence we get the value of $\angle AOC$ as
$\therefore \angle AOC = {90^ \circ }$
As we know that an angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
According to the above statement we get the equation as
$\therefore \angle ADC = \dfrac{1}{2}\angle AOC$
Now we put the value of $\angle AOC$ in the above equation, we get
$\therefore \angle ADC = \dfrac{1}{2} \times {90^ \circ }$
By solving the above equation we get the value of $\angle ADC$ as,
$\therefore \angle ADC = {45^ \circ }$

So, the value of the $\angle ADC$ is ${45^ \circ }$.

So, the correct answer is “Option C”.

Note: In these type of questions first we detect which angle is formed at the center and which is made in the remaining part of the circle. And after this we should apply the theorem which made our calculation easy. And remember that if we find the value of the angle made at the center we double the value of the angle made in the remaining part. And if we are finding the value of the angle made in the remaining part of the circle we should half the value of the angle made at the center of the circle.