Question

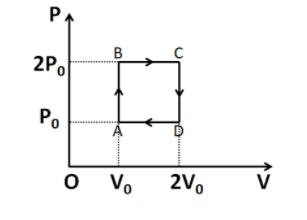
Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure. Efficiency of this cycle is nearly (assume the gas to be close to ideal gas)

(A) $15.4\%$
(B) $9.1\%$
(C) $10.5\%$
(D) $12.5\%$

Answer 1

The efficiency of a cycle is equal to the ratio of the work done in that cycle to the heat absorbed. The work done can be easily evaluated by calculating the area of the P-V diagram given in the question.

Complete step-by-step solution:
We know that the work done in a process is equal to the area of the P-V diagram. So the work done in the given cycle is given by
$W = Ar\left( {ABCD} \right)$
$\Rightarrow W = AB \times AD$
From the given diagram, we have $AB = {P_0}$ and $AD = {V_0}$. Substituting these above, we get
$W = {P_0}{V_0}$.....................(1)
Since the direction of the loop is clockwise, so the work done is positive.
Now, the heat is absorbed in the processes AB and BC. These two respectively are isochoric and isobaric processes. So we have
${Q_{AB}} = n{C_V}\Delta T$
We know that ${C_V} = \dfrac{{fR}}{2}$. So we have
${Q_{AB}} = \dfrac{{fnR\Delta T}}{2}$
$\Rightarrow {Q_{AB}} = \dfrac{{fV\Delta P}}{2}$ (1) (from the ideal gas equation for constant pressure)
For the process AB, we have
$\Delta P = 2{P_0} - {P_0}$
$\Rightarrow \Delta P = {P_0}$
Also $V = {V_0}$
Substituting these in (1) we get
${Q_{AB}} = \dfrac{{f{P_0}{V_0}}}{2}$....................(2)
Now, for the process BC, we have
${Q_{BC}} = n{C_P}\Delta T$
We know that ${C_P} = \left( {\dfrac{f}{2} + 1} \right)R$. So we have
${Q_{BC}} = \left( {\dfrac{f}{2} + 1} \right)nR\Delta T$
$\Rightarrow {Q_{BC}} = \left( {\dfrac{f}{2} + 1} \right)P\Delta V$................(3) (from the ideal gas equation for constant pressure)
For the process BC we have
$\Delta V = 2{V_0} - {V_0}$
$\Rightarrow \Delta V = {V_0}$
Also $P = 2{P_0}$
Substituting these in (3) we get
${Q_{BC}} = 2\left( {\dfrac{f}{2} + 1} \right){P_0}{V_0}$....................(4)
Adding (2) and (4) we get the total heat absorbed as
$Q = \dfrac{{f{P_0}{V_0}}}{2} + 2\left( {\dfrac{f}{2} + 1} \right){P_0}{V_0}$
$\Rightarrow Q = {P_0}{V_0}\left[ {\dfrac{f}{2} + 2\left( {\dfrac{f}{2} + 1} \right)} \right]$
Now, since Helium is a monatomic gas, we have $f = 3$. Substituting this above, we get
$Q = {P_0}{V_0}\left[ {\dfrac{3}{2} + 2\left( {\dfrac{3}{2} + 1} \right)} \right]$
$\Rightarrow Q = \dfrac{{13}}{2}{P_0}{V_0}$......................(5)
Now, the efficiency is given by
$\eta = \dfrac{W}{Q}$
Putting (1) and (5) we get
$\eta = \dfrac{{{P_0}{V_0}}}{{\dfrac{{13}}{2}{P_0}{V_0}}}$
$\Rightarrow \eta = \dfrac{2}{{13}} \approx 0.154$
Multiplying by $100$, we get the percentage efficiency of the cycle equal to $15.4\%$.

Hence, the correct answer is option (1).

Note: The sign of the work done is very much important. It can be easily found out by using the direction of the loop of the cycle in a P-V diagram. A clockwise loop means a positive work, while an anticlockwise loop means a negative work.