Question

Half of the uniform rectangular plate of length ‘L’ is made up of material of density ${d}_{1}$ and the other half with density ${d}_{2}$. The perpendicular distance of mass from AB is

A. $\dfrac {2{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}} \times \dfrac {L}{4}$
B. $\dfrac {{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}} \times \dfrac {L}{4}$
C. $\dfrac {3{d}_{1}}{{d}_{1}+{d}_{2}} \times \dfrac {L}{4}$
D. $\dfrac {3{d}_{2}}{{d}_{1}+{d}_{2}} \times \dfrac {L}{4}$

Answer 1

To solve this question, first find the mass of each half of the plate in terms of density and volume. Then, substitute the value of volume in terms of area and thickness. Find the distance of center of mass for both halves of the plate. Then, use the formula for position of center of mass, Substitute the values in the formula and find the perpendicular distance of the mass from AB.
Formula used:
$Density= \dfrac {Mass}{Volume}$
$V= At$
${X}_{CM}= \dfrac {{m}_{1}{x}_{1}+{m}_{2}{x}_{2}}{{m}_{1}+{m}_{2}}$

Complete answer:

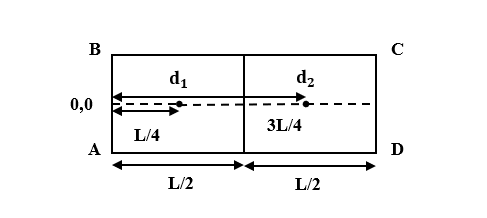
Given: Length of the rectangular plate= L
Density of materials are ${d}_{1}$ and ${d}_{2}$ respectively.
The formula for density is given by,
$Density= \dfrac {Mass}{Volume}$
$\Rightarrow d= \dfrac {m}{V}$ …(1)
Where, d is the density of the plate
m is the mass of the plate
V is the volume of the plate
Let the area of the rectangular plate be A
The thickness of the plate be t
We know, volume of a rectangular plate is given by,
$V= At$ …(2)
Where, V is the volume of the rectangular plate
A is the area off the plate
t is the thickness of the plate
Substituting equation. (2) in equation. (1) we get,
$d= \dfrac {m}{At}$
Density of first half of the plate can be given by,
${d}_{1}= \dfrac {{m}_{1}}{\dfrac {At}{2}}$
$\Rightarrow {m}_{1}={d}_{1}\dfrac {At}{2}$
Similarly, the density of second half of the plate can be given by,
${d}_{2}= \dfrac {{m}_{2}}{\dfrac {At}{2}}$
$\Rightarrow {m}_{2}={d}_{2}\dfrac {At}{2}$
From the diagram we can infer, ${x}_{1}= \dfrac {L}{4}$ and ${x}_{2}= \dfrac{3L}{4}$.
The position for center of mass is given by,
${X}_{CM}= \dfrac {{m}_{1}{x}_{1}+{m}_{2}{x}_{2}}{{m}_{1}+{m}_{2}}$
Substituting values in above equation we get,
${X}_{CM}= \dfrac {{d}_{1}(\dfrac {At}{2})\dfrac {L}{4}+ {d}_{2}(\dfrac {At}{2})\dfrac {3L}{4}}{{ d}_{1}\dfrac {At}{2}+ { d}_{2}\dfrac {At}{2}}$
$\Rightarrow {X}_{CM}= \dfrac {\dfrac {{d}_{1}AtL+ 3{d}_{2}AtL}{8}}{\dfrac {{d}_{1}At+{d}_{2}At}{2}}$
$\Rightarrow {X}_{CM}= \dfrac {2}{8} . (\dfrac {{d}_{1}AtL+ 3{d}_{2}AtL}{{d}_{1}At+ {d}_{2}At})$
$\Rightarrow {X}_{CM}= \dfrac {2AtL}{8At} .\dfrac {{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}}$
$\Rightarrow {X}_{CM}= \dfrac {L}{4} .\dfrac {{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}}$
Hence, the perpendicular distance of mass from AB is $\dfrac {L}{4} .\dfrac {{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}}$.

So, the correct answer is option B i.e. $\dfrac {{d}_{1}+3{d}_{2}}{{d}_{1}+{d}_{2}} \times \dfrac {L}{4}$

Note:
Students must understand that if they do not substitute the value of volume in terms of area and thickness, still they will get the same answer as the term At gets cancelled any way. So, if they don’t write that step, the length of the solution gets reduced. Students must try to solve a given problem in a shorter method, this will save their time and they can go to the next question.