Question

Let the expression inside the 9th root be $E$. $E = 4\sin^4x-6\sin^2x+2-2\cos^2x-\frac{1}{2}\cos4x-x^9$ Using trigonometric identities: $\cos^2x = 1 - \sin^2x$ $\sin^2x = \frac{1-\cos2x}{2}$ $\cos4x = 2\cos^22x - 1$

Substitute $\cos^2x = 1-\sin^2x$ into $E$: $E = 4\sin^4x-6\sin^2x+2-2(1-\sin^2x)-\frac{1}{2}\cos4x-x^9$ $E = 4\sin^4x-4\sin^2x-\frac{1}{2}\cos4x-x^9$

Substitute $\sin^2x = \frac{1-\cos2x}{2}$ and $\cos4x = 2\cos^22x-1$: $4\sin^4x = 4\left(\frac{1-\cos2x}{2}\right)^2 = 1-2\cos2x+\cos^22x$ $4\sin^2x = 4\left(\frac{1-\cos2x}{2}\right) = 2-2\cos2x$

Substitute these into $E$: $E = (1-2\cos2x+\cos^22x) - (2-2\cos2x) - \frac{1}{2}(2\cos^22x-1) - x^9$ $E = 1-2\cos2x+\cos^22x - 2+2\cos2x - \cos^22x+\frac{1}{2} - x^9$ $E = (1-2+\frac{1}{2}) + (-2\cos2x+2\cos2x) + (\cos^22x-\cos^22x) - x^9$ $E = -\frac{1}{2} - x^9$

Thus, the function simplifies to $g(x) = \left(-\frac{1}{2} - x^9\right)^{1/9}$.

Let $y = g(2025)$. Then $y = \left(-\frac{1}{2} - 2025^9\right)^{1/9}$, which implies $y^9 = -\frac{1}{2} - 2025^9$. Now, we evaluate $g(g(2025)) = g(y)$: $g(y) = \left(-\frac{1}{2} - y^9\right)^{1/9}$ Substitute the expression for $y^9$: $g(y) = \left(-\frac{1}{2} - \left(-\frac{1}{2} - 2025^9\right)\right)^{1/9}$ $g(y) = \left(-\frac{1}{2} + \frac{1}{2} + 2025^9\right)^{1/9}$ $g(y) = \left(2025^9\right)^{1/9} = 2025$.

The sum of digits of $g(g(2025))$ is the sum of digits of 2025. Sum of digits = $2 + 0 + 2 + 5 = 9$.

75. Let $A = \begin{bmatrix} 2 & 0 \\ 0 & -3 \end{bmatrix}$, $B = \begin{bmatrix} 0 & 3 \\ 1 & 0 \end{bmatrix}$ and

$X = \begin{bmatrix} cosx & -sinx \\ sinx & cosx \end{bmatrix}$. If $P = AXB^T$ and

$Q = B^TX^TA$, then number of positive integral divisors of det $(PQ)$ is

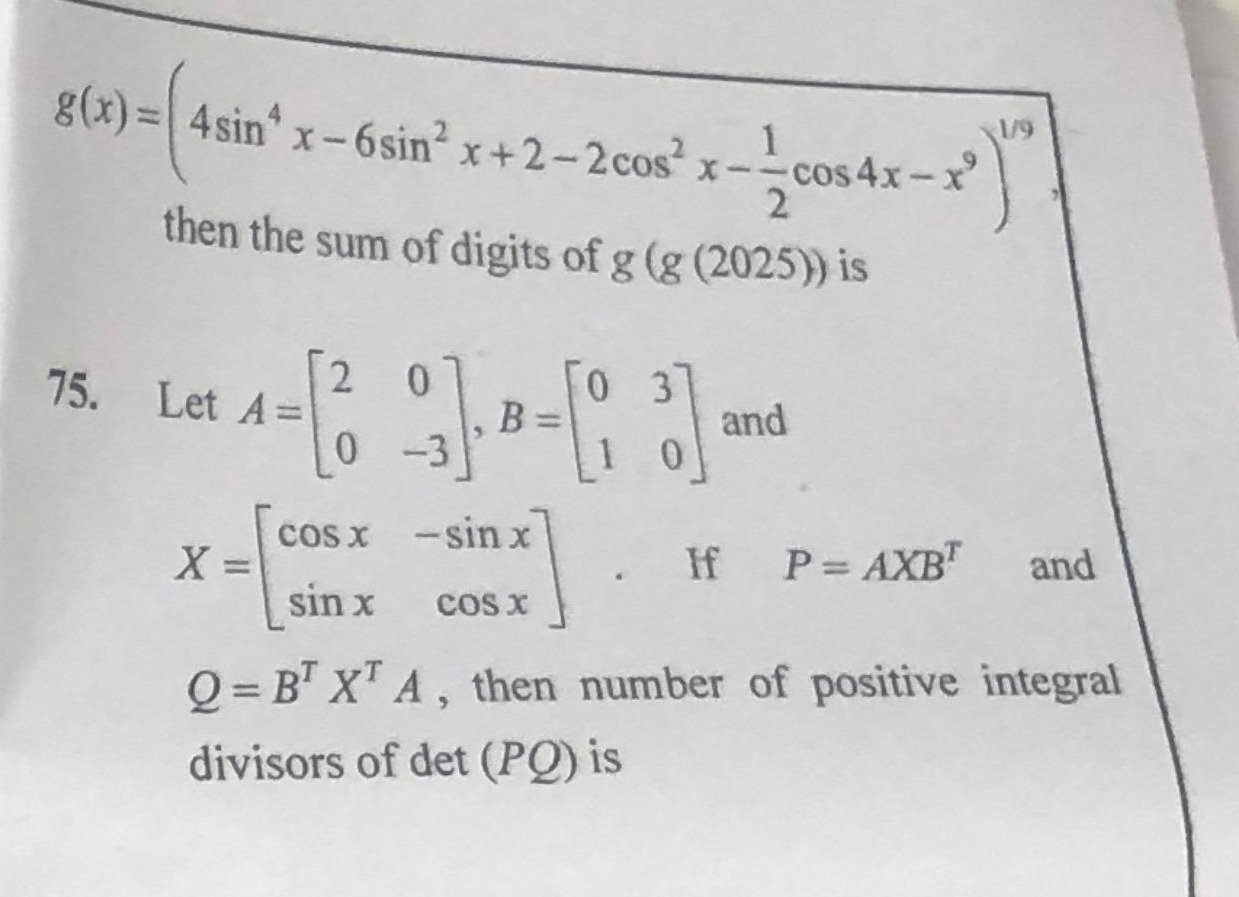
• A. 9
• B. 15
• C. 24
• D. 30

Answer 1

Answer: (A), (B)

The question contains two independent problems. The first problem asks for the sum of the digits of $g(g(2025))$, which is 9. The second problem asks for the number of positive integral divisors of $\det(PQ)$, which is 15.

Answer 2

Problem 1: The function $g(x)$ simplifies to $g(x) = \left(-\frac{1}{2} - x^9\right)^{1/9}$. Evaluating $g(g(2025))$ results in 2025. The sum of the digits of 2025 is $2+0+2+5 = 9$.

Problem 2: Given matrices $A = \begin{bmatrix} 2 & 0 \\ 0 & -3 \end{bmatrix}$, $B = \begin{bmatrix} 0 & 3 \\ 1 & 0 \end{bmatrix}$, and $X = \begin{bmatrix} \cos x & -\sin x \\ \sin x & \cos x \end{bmatrix}$. $\det(A) = -6$ $\det(B) = -3$ $\det(X) = 1$

$P = AXB^T \implies \det(P) = \det(A)\det(X)\det(B^T) = (-6)(1)(-3) = 18$. $Q = B^TX^TA \implies \det(Q) = \det(B^T)\det(X^T)\det(A) = (-3)(1)(-6) = 18$.

$\det(PQ) = \det(P)\det(Q) = 18 \times 18 = 18^2$. The prime factorization of 18 is $2 \times 3^2$. So, $18^2 = (2 \times 3^2)^2 = 2^2 \times 3^4$. The number of positive integral divisors is $(2+1)(4+1) = 3 \times 5 = 15$.