Question

Graphs between pressure and volume are plotted at different temperatures. Which of the following isotherms represents Boyle’s law as ${\text{PV}} = {\text{Constant}}$?

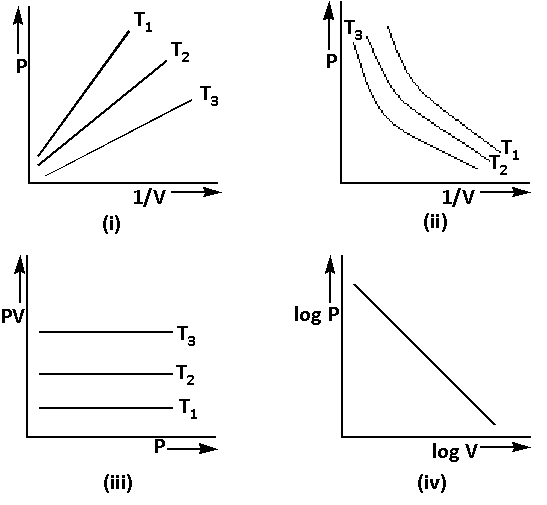
A) Only (ii) is a correct representation of Boyle’s law.
B) Only (iv) is the correct representation of Boyle’s law.
C) All are correct representations of Boyle’s law.
D) None of these representations is correct for Boyle’s law.

Answer 1

To solve this we must know Boyle's law. Boyle’s law states that at constant temperature the volume of an ideal gas is inversely proportional to the pressure of the gas.

Complete step by step answer:
We know that Boyle's law states that at constant temperature the volume of an ideal gas is inversely proportional to the pressure of the gas.
The expression for Boyle’s law is as follows:
${\text{P}} \propto \dfrac{1}{{\text{V}}}$ …… (1)
Where ${\text{P}}$ is the pressure,
${\text{V}}$ is the volume.
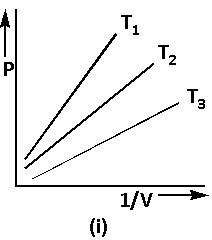
Using equation (1), the graph of Boyle’s law is as follows:

The equation (1) can be written as follows:
${\text{P}} = {\text{K}}\dfrac{1}{{\text{V}}}$ …… (2)
Where ${\text{K}}$ is the constant.
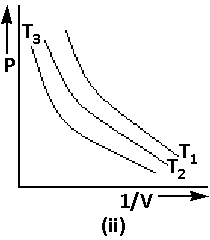
Using equation (2), the graph of Boyle’s law is as follows:

We are given that ${\text{PV}} = {\text{Constant}}$. Thus,
${\text{PV}} = {\text{K}}$ …… (3)
The equation (3) can also be written as follows:
${\text{PV}} = \dfrac{{\text{K}}}{{\text{P}}} \times {\text{P}}$ …… (4)

Using equation (4), the graph of Boyle’s law is as follows:

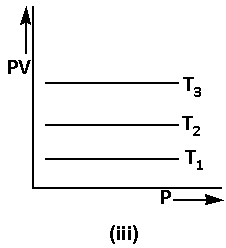
The equation (2) can be written in the form of log as follows:
${\text{log P}} = - \log {\text{ V}} + \log {\text{ K}}$ …… (5)
Using equation (5), the graph of Boyle’s law is as follows:

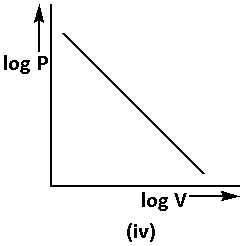
From the above graphs, we can say that all the graphs are the correct representations of Boyle’s law.
Thus, the correct option is (C).

Note: We know that Boyle's law states that at constant temperature the volume of an ideal gas is inversely proportional to the pressure of the gas. Thus, as the volume of the gas increases, the pressure decreases or as the volume of the gas decreases, the pressure increases.