Question

Graph $y = 2{\left( {x - 1} \right)^2} + 4$?

Answer 1

The equation in the question represents a parabola, and we have to graph the parabola for this we will find the intercepts and we will assume one variable as zero to find the value of other variable i.e., if we have to find variable $x$ we have to assume $y=0$, and if we have to find variable $y$ we have to assume $x = 0$, and to find the vertex of the parabola, transform the equation into the vertex form i.e., $y = a{\left( {x - h} \right)^2} + k$, where$\left( {h,k} \right)$ is the vertex of the parabola, now plot the points on the graph, to get the required graph.

Complete step by step answer:
Given the equation is $y = 2{\left( {x - 1} \right)^2} + 4$, from the equation we are given that the equation represents a parabola and the parabola does not pass through the origin.
Now to find the intercepts we have assume one variable as zero to find the value of other variable i.e., if we have to find variable $x$ we have to assume $y = 0$, and if we have to find variable $y$ we have to assume $x = 0$.
So, here put $x = 0$, we get,
$\Rightarrow y = 2{\left( {0 - 1} \right)^2} + 4$,
$\Rightarrow y = 2{\left( {- 1} \right)^2} + 4$,
$\Rightarrow y = 2\left( 1 \right) + 4$,
$\Rightarrow y = 2 + 4 = 6$,
So y-intercept of the parabola is $\left( {0,6} \right)$.
Now substitute $y = 0$ to find the intercept of$x$,
$\Rightarrow 0 = 2{\left( {x - 1} \right)^2} + 4$,
Now subtract 4 from the both sides we get,
$\Rightarrow 0 - 4 = 2{\left( {x - 1} \right)^2} + 4 - 4$,
$\Rightarrow - 4 = 2{\left( {x - 1} \right)^2}$,
Now divide both sides of the equation with 2 we get,
$\Rightarrow \dfrac{{2{{\left( {x - 1} \right)}^2}}}{2} = \dfrac{{ - 4}}{2}$,
$\Rightarrow {\left( {x - 1} \right)^2} = - 2$
Now taking the square root we get,
$\Rightarrow \left( {x - 1} \right) = \sqrt { - 2}$,
So, we know that square root of the negative number does not exist, therefore there will be no-intercepts for the given function,
Now to find the vertex of the parabola, compare the equation into the vertex form i.e., $y = a{\left( {x - h} \right)^2} + k$, where$\left( {h,k} \right)$ is the vertex of the parabola,
So here the equation is $y = 2{\left( {x - 1} \right)^2} + 4$,
Now comparing the equations we get, $a = 2, h = 1$ and $k = 4$,
So the vertex of the parabola is $\left( {1,4} \right)$,
If we plot the parabola, we get the graph as,

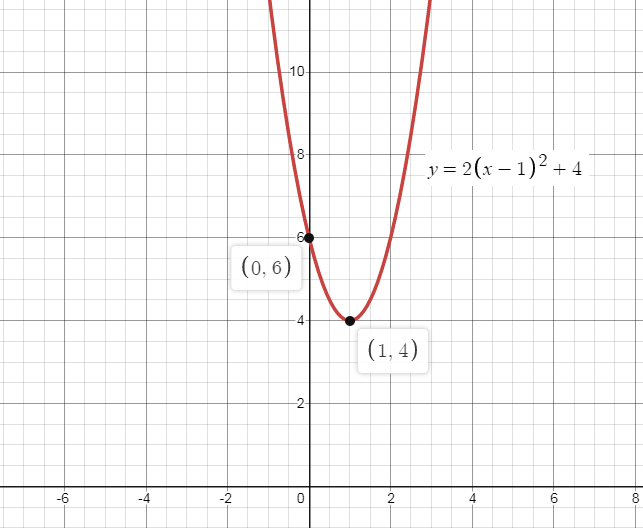
$\therefore$ The vertex of the parabola $y = 2{\left( {x - 1} \right)^2} + 4$ is $\left( {1,4} \right)$, the y-intercept of the parabola is $\left( {0,6} \right)$ and there are no x-intercepts, and the required graph will be

Note: Symmetric points are called the points which are equidistant from the axis of symmetry and lie on the x-axis and they are calculated as x-intercepts. To find the vertex of the parabola we can also make use of the standard form of the equation $y = ax^2+bx+c$, where the axis of symmetry or the x-coordinate is given by $x=-\dfrac{b}{2a}$ and then we will find the value of $y$ from the equation of the parabola.