Question

Graph the trigonometric equation $y = 3\cos x$

Answer 1

Hint : If in an equation, there are one or more than one trigonometric ratios [sine $\left( {\sin } \right)$ , cosine $\left( {\cos } \right)$ , tangent $\left( {\tan } \right)$ , cotangent $\left( {\cot } \right)$ , secant $\left( {\sec } \right)$ , cosecant $\left( {\cos ec} \right)$ ] of unknown angles, it is said to be trigonometric equation and here, we have to make a graph of the given trigonometric equation.

Complete step-by-step answer :
To make a graph of the trigonometric equation, we have a function, $f\left( x \right) = a\cos b\left( {x + c} \right) + d$
On comparing the function $y = 3\cos x$ with the above function, we have found that only the parameter a, means $3$ will affect our function. Now, let us assume the values of x in the function $f\left( x \right)$ which is equal to y.
Part-1 Let us assume the value of x be $0$ , then the function $f\left( x \right)$ becomes,
$f\left( 0 \right) = 3\cos \left( 0 \right) = 3 \times 1 = 3$
And we know that, $f\left( x \right) = y$ , then the value of y becomes $3$ .
Part-2 Let us assume the value of x be $\dfrac{\pi }{6}$ , then the function $f\left( x \right)$ becomes,
$f\left( {\dfrac{\pi }{6}} \right) = 3\cos \left( {\dfrac{\pi }{6}} \right) = 3 \times \left( {\dfrac{{\sqrt 3 }}{2}} \right) = \dfrac{{3\sqrt 3 }}{2}$
And we know that, $f\left( x \right) = y$ , then the value of y becomes $\dfrac{{3\sqrt 3 }}{2}$ .
Part-3 Let us assume the value of x be $\dfrac{\pi }{4}$ , then the function $f\left( x \right)$ becomes,
$f\left( {\dfrac{\pi }{4}} \right) = 3\cos \left( {\dfrac{\pi }{4}} \right) = 3 \times \dfrac{1}{{\sqrt 2 }} = \dfrac{3}{{\sqrt 2 }}$
And we know that, $f\left( x \right) = y$ , then the value of y becomes $\dfrac{3}{{\sqrt 2 }}$ .
Part-4 Let us assume the value of x be $\dfrac{\pi }{2}$ , then the function $f\left( x \right)$ becomes,
$f\left( {\dfrac{\pi }{2}} \right) = 3\cos \left( {\dfrac{\pi }{2}} \right) = 3 \times 0 = 0$
And we know that, $f\left( x \right) = y$ , then the value of y becomes $0$ .
Part-5 Let us assume the value of x be $\pi$ , then the function $f\left( x \right)$ becomes,
$f\left( \pi \right) = 3\cos \left( \pi \right) = 3 \times \left( { - 1} \right) = - 3$
And we know that, $f\left( x \right) = y$ , then the value of y becomes $- 3$ .
Hence, we have our values of x and y to plot the graph of $y = 3\cos x$ and the graph is,

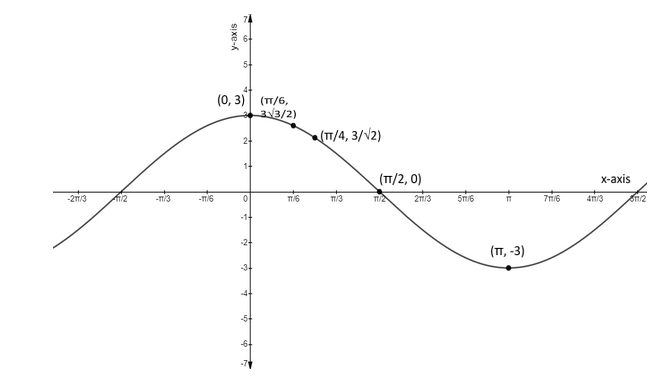
Note : To form a graph of cosine function, there is an equation i.e, $f\left( x \right) = a\cos b\left( {x + c} \right) + d$ , where, a is the amplitude of the function, b affects the period as it is equal to $\dfrac{{2\pi }}{b}$ , if the value of b increases then the value of period decreases, c is the horizontal shift and d is the principal axis. The graph of the given trigonometric equation is quite easy to solve as only $3$ is affecting the function.