Question
Question: Graph the given inequality equation \[y < 3x - \dfrac{3}{4}\]?...
Graph the given inequality equation y<3x−43?
Solution
For any inequality when you are solving you should know the sign of inequality changes when you multiply minus sign both the side, and rest solution can be done same as that for equals sign is done, nor any other assumption should be needed. In case of graphs you should know that graphs give a region of space in the coordinate axis where the function given satisfies every value of that space.
Complete step by step solution:
For the given inequality y<3x−43
For finding the coordinates we have to remove inequality sign and put equals to just for finding the coordinates, we get;
⇒y=3x−43
Now assuming any two coordinate for”x” as “(0 and 1)” respective coordinates for “y” are:
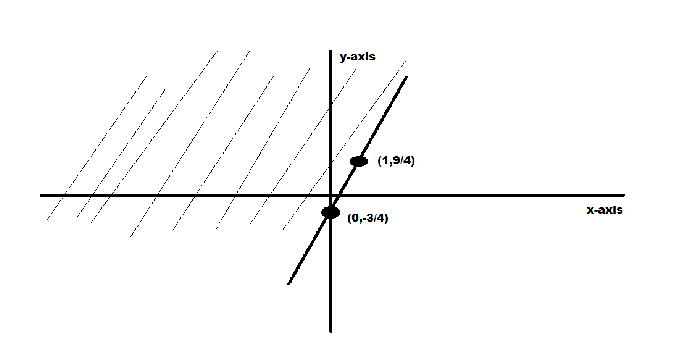
⇒forx=0,1y=−43,(3×1−43) ⇒y=−43,(3−43) ⇒y=−43,(43×4−3) ⇒y=−43,(49)Now plotting graph with the given coordinates that is:
⇒(x,y)=(0,−43),(1,49)
Here for the region accessed by graph we have to check with the inequality in which we can put any coordinate from left side of the line drawn or from the right side, the one coordinate which will satisfies the inequality will be the required area for the given question, on solving we get,
Putting(x,y)=(0,0)i.e.fromleftsideoflineweget ⇒y<3(0)−43 ⇒y<−43whichistruehenceleftsideareaoftheobtainedlineingraphisourrequiredarea.We get:
Note: Inequality basically defines the region of the quantity whosoever for which the inequality is used for, that is it gives you a range of possible values for the quantity you are finding for. In this range real as also complex range also occurs. In graph you should the region you are dealing with and for confirming your solution you can check for any value in the region of graph that it will satisfy the
equation.
