Question

Graph the function $y = \cos 2x$?

Answer 1

In this question, first we have to find the period and amplitude of the given function, and then take some values for $x$ and then find the respective $y$ for each $x$, then tabulate the values and with help of the table we will get the required graph.

Complete step-by-step answer:
The graph of $y = \cos x$ is like a wave that forever oscillates between. $- 1$ and $1$, in a shape that repeats itself every $2\pi$ units. Specifically, this means that the domain of $\cos x$ is all real numbers, and the range is $\left[ { - 1,1} \right]$.
Now given function is $y = \cos 2x$,
Use the form $y = a\sin \left( {bx - c} \right) + d$ to find the variables used to find the amplitude, period, phase shift, and vertical shift.
$a = 1$,$b = 2$,$c = 0$, and $d = 0$,
So here amplitude $a = 1$,
Now period of the function is given by, $\dfrac{{2\pi }}{{\left| b \right|}}$ from the given data,
So, substituting the value of $b = 2$ in the period formula, we get,
$\Rightarrow \dfrac{{2\pi }}{{\left| 2 \right|}} = \pi$,
Period of the given function will be $\pi$,
Now select some values to graph the function,
When $x = 0$,
\Rightarrow $$$$y = \cos 2x,
Now simplifying we get,
$\Rightarrow y = \cos 2\left( 0 \right)$,
Now simplifying we get,
$y = \cos 0 = 1$
When $x = \dfrac{\pi }{2}$,
$\Rightarrow y = \cos 2\left( {\dfrac{\pi }{2}} \right)$,
Now simplifying we get,
$\Rightarrow y = \cos \pi = - 1$,
When $x = \pi$,
$\Rightarrow y = \cos 2\left( \pi \right)$,
Now simplifying we get,
$\Rightarrow y = \cos 2\pi = 1$,
When $x = \dfrac{{3\pi }}{2}$,
$\Rightarrow y = \cos 2\left( {\dfrac{{3\pi }}{2}} \right)$,
Now simplifying we get,
$\Rightarrow y = \cos 3\pi = - 1$,
When $x = 2\pi$,
$\Rightarrow y = \cos 2\left( {2\pi } \right)$,
Now simplifying we get,
$\Rightarrow y = \cos 4\pi = 1$,
Now tabulating the values we get,

$x$	$y$
0	1
$\dfrac{\pi }{2}$	-1
$\pi$	1
$\dfrac{{3\pi }}{2}$	-1
$2\pi$	1

Now plotting the graphs we get,

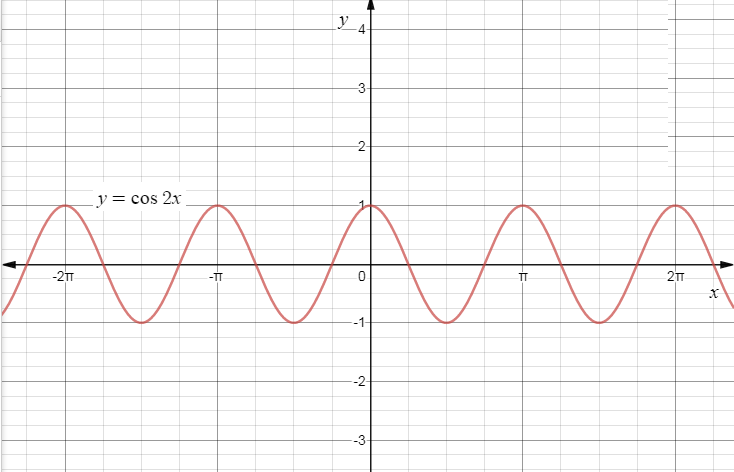
$\therefore$The required graph for the function $y = \cos 2x$ is,

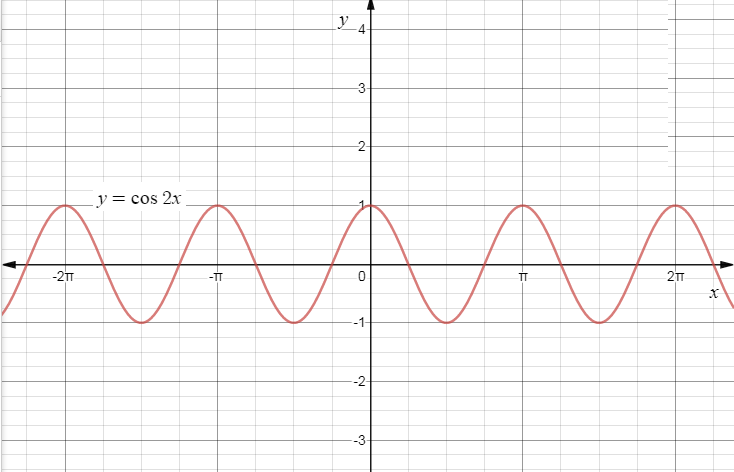
Note:
To graph the cosine function, we mark the angle along the horizontal x axis, and for each angle, we put the cosine of that angle on the vertical y-axis. The graph, as seen above, is a smooth curve that varies from +1 to -1. It is the same shape as the cosine function but displaced to the left ${90^o}$. Curves that follow this shape are called 'sinusoidal' after the name of the sine function whose shape it resembles.