Question

Graph the following trigonometric equation, $y = 2\sin \left( {\dfrac{x}{3}} \right)$ .

Answer 1

Hint : To draw the graph of the trigonometric functions (sine, cosine and tangent), we need to know the amplitude, the period and the phase shift of the given trigonometric equation. The value of amplitude is always positive and it is the coefficient of the given trigonometric function.

Complete step by step solution:
Firstly, we will find the amplitude of the trigonometric equation, $y = 2\sin \left( {\dfrac{x}{3}} \right)$ , and the amplitude is 2.
Secondly, the period is calculated by taking $2\pi$ and dividing it with the coefficient of x. So, period becomes,
$\left( {\dfrac{{2\pi }}{{\dfrac{1}{3}}}} \right) = 2\pi \times \dfrac{3}{1} = 6\pi$
Now, to sketch the graph, we need the phase shift and phase shift is calculated by taking Angle $= 0$ , here the angle is $\dfrac{x}{3}$ , now, the phase shift becomes $0$ .
$\Rightarrow \dfrac{x}{3} = 0 \\\ \Rightarrow x = 0 \;$
Now, we need to calculate the quarter of the period $(QP)$ and in order to calculate the quarter of the period the value of the period is divided by $4$ .
$\Rightarrow QP = \dfrac{{6\pi }}{4} \\\ \Rightarrow QP = \dfrac{{3\pi }}{2} \;$
Now, we have to calculate the values of x.
${x_1} = 0$
As, the first x is equal to the phase shift. Now, we will substitute the value of x in the equation given above.
$\Rightarrow y = 2\sin \left( {\dfrac{x}{3}} \right) \\\ \Rightarrow {y_1} = 2\sin \left( {\dfrac{0}{3}} \right) \\\ \Rightarrow {y_1} = 0 \;$ .
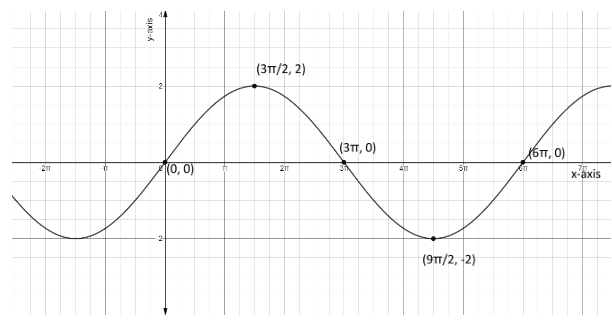
Now, our first point $\left( {{x_1},{y_1}} \right)$ is $\left( {0,0} \right)$ .
${x_2} =$ the sum of the value of the first x and the value of the quarter of the period
$\Rightarrow {x_2} = {x_1} + QP \\\ \Rightarrow {x_2} = 0 + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_2} = \dfrac{{3\pi }}{2} \;$
Now, we will substitute the value of the second x into the given equation to find the value of second y.
$y = 2\sin \left( {\dfrac{x}{3}} \right) \\\ \Rightarrow {y_2} = 2\sin \left( {\dfrac{{3\pi }}{2} \times \dfrac{1}{3}} \right) \\\ \Rightarrow {y_2} = 2\sin \left( {\dfrac{\pi }{2}} \right) \\\ \Rightarrow {y_2} = 2 \;$
Now, the second point $\left( {{x_2},{y_2}} \right)$ is $\left( {\dfrac{{3\pi }}{2},2} \right)$ . $$
${x_3} =$ the sum of the value of second x and the value of the quarter of the period
$\Rightarrow {x_3} = {x_2} + QP \\\ \Rightarrow {x_3} = \dfrac{{3\pi }}{2} + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_3} = \dfrac{{6\pi }}{2} \\\ \Rightarrow {x_3} = 3\pi \;$
Now, we will substitute the value of third x in the given equation to find the value of the third y.
$y = 2\sin \left( {\dfrac{x}{3}} \right) \\\ \Rightarrow {y_3} = 2\sin \left( {\dfrac{{3\pi }}{3}} \right) \\\ \Rightarrow {y_3} = 2\sin \pi \\\ \Rightarrow {y_3} = 0 \;$
Now, the third point $\left( {{x_3},{y_3}} \right)$ is $\left( {3\pi ,0} \right)$ .
${x_4} =$ the sum of the value of third x and the value of the quarter of the period
$\Rightarrow {x_4} = {x_3} + QP \\\ \Rightarrow {x_4} = 3\pi + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_4} = \dfrac{{3\pi \times 2}}{{1 \times 2}} + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_4} = \dfrac{{6\pi }}{2} + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_4} = \dfrac{{9\pi }}{2} \;$
Now, we will substitute the value of fourth x in the given equation to find the value of the fourth y.
$y = 2\sin \left( {\dfrac{x}{3}} \right) \\\ \Rightarrow {y_4} = 2\sin \left( {\dfrac{{9\pi }}{2} \times \dfrac{1}{3}} \right) \\\ \Rightarrow {y_4} = 2\sin \left( {\dfrac{{3\pi }}{2}} \right) \\\ \Rightarrow {y_4} = - 2 \;$
Now, the fourth point $\left( {{x_4},{y_4}} \right)$ is $\left( {\dfrac{{9\pi }}{2}, - 2} \right)$
${x_5} =$ the sum of the value of fourth x and the value of the quarter of the period
$\Rightarrow {x_5} = {x_4} + QP \\\ \Rightarrow {x_5} = \dfrac{{9\pi }}{2} + \dfrac{{3\pi }}{2} \\\ \Rightarrow {x_5} = \dfrac{{12\pi }}{2} \\\ \Rightarrow {x_5} = 6\pi \;$
Now, we will substitute the value of fifth x in the given equation to find the value of fifth y.
$y = 2\sin \left( {\dfrac{x}{3}} \right) \\\ \Rightarrow {y_5} = 2\sin \left( {\dfrac{{6\pi }}{3}} \right) \\\ \Rightarrow {y_5} = 2\sin \left( {2\pi } \right) \\\ \Rightarrow {y_5} = 0 \;$
Now, the fifth point $\left( {{x_5},{y_5}} \right)$ is $\left( {6\pi ,0} \right)$ .
Hence, the graph formed of the given equation is,

Note : In this problem, to make a graph, firstly we have find the amplitude, period, phase shift and the quarter of the period and with the help of the quarter of the period, we have found the values of x and with the help of the values of x, we found the values of y and with the help of the values of x and y, we have plotted the points on the graph and after plotting the values, we have joined the points with each other in order to make a graph.