Question

Graph the following equation, $y = \dfrac{3}{4}x - 4$ and explain the steps for the same.

Answer 1

The standard equation of a line in slope-intercept form is,$y = mx + c$ where “m” is the slope of the line and “c” is the y intercept of the line. Compare the given equation in the question and find the value of the slope and the y-intercept. After the values are found, analyze the slope. If the value of “m” is less than 0 then the line will be downwards. If the value of “m” is greater than 0 then the line will be in the upwards direction from left to right.

Complete step by step solution:
The standard equation of a line in the slope-intercept form is, $y = mx + c$ where “m” is the slope of the line and “c” is the y intercept of the line. Comparing $y = \dfrac{3}{4}x - 4$ with the standard equation, we get $m = \dfrac{3}{4}$ and $c = - 4$.
Since we see that, $m > 0$, the line will be in the upwards direction from left to right.
Now that we have all the information about the line, we need to find the coordinates to plot the Let $x = 0$,
Putting the value in the line equation, $y = (\dfrac{3}{4} \times 0) - 4 = - 4$.
Now, let $y = 0$, hence by putting the value in the line equation, we get

$$x = (0 + 4) \times \dfrac{4}{3} \\\ \Rightarrow x = 4 \times \dfrac{4}{3} \\\ \Rightarrow x = \dfrac{{16}}{3} \\\$$

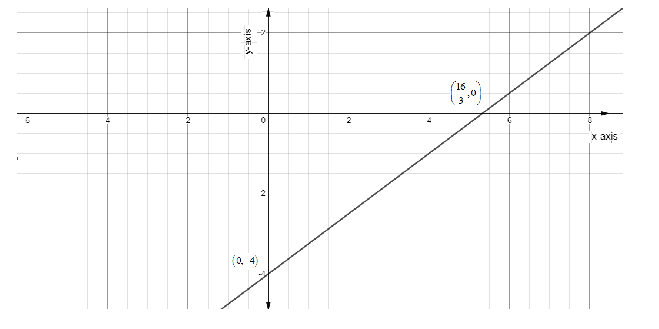
Thus, we have 2 coordinated of the line $y = \dfrac{3}{4}x - 4$ as (0, - 4)\ & (\dfrac{{16}}{3},0).
Plotting these 2 points on the graph and drawing a line joining them and extending them on both sides will give us the graph for $y = \dfrac{3}{4}x - 4$.
The graph will look like,

Note: There are 2 forms in which line equations can be expressed. Namely, point-slope and slope- intercept form. In case of point-slope form, as the name itself suggests contains information about one coordinate and the slope of the line. It is written in the form $y - {y_1} = m(x - {x_1})$, where m is the slope and $({x_1},{y_1})$ are the coordinates.