Question

Graph shows a hypothetical speed distribution for a sample of $N$ gas particle (for $V > {V_0}$​;$\dfrac{{dN}}{{dV}} = 0$,$\dfrac{{dN}}{{dV}}$​ is a rate of change of number of particles with change velocity.)

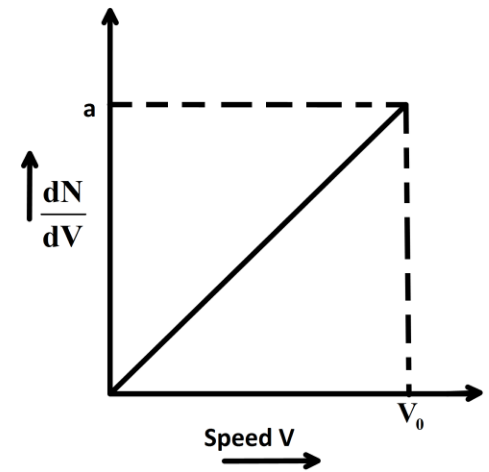
A. The value of $a{V_0}$ is $2N$
B. The ratio of $\dfrac{{{V_{avg}}}}{{{V_0}}}$ is equal to $\dfrac{2}{3}$
C. The ratio of $\dfrac{{{V_{rms}}}}{{{V_0}}}$ is equal to $\dfrac{1}{{\sqrt 2 }}$
D. Three fourth of the total particle has a speed between $0.5{V_0}$and ${V_0}$

Answer 1

To solve this problem find the value of the rate of change of number of particles with change in velocity. Then find the relation between the ${V_0}$ and the number of particles $N$.

Formula used:
The equation of straight line is given by,
$y = mx + c$
where, $m$ is the slope of the straight line and $c$ is the interception on the Y-axis.

Complete step by step answer:
From the graph we can see that the slope of the curve is, $\dfrac{a}{{{V_0}}}$ since the maximum value of Y-axis is $a$ and on the X-axis it is ${V_0}$ minimum value is zero. The interception on the Y-axis is zero. The Y variable is here the rate of change of number of particles with change in velocity $\dfrac{{dN}}{{dV}}$ and the X-axis plot is ${V_0}$.

Hence, we can write the equation of the curve as, $\dfrac{{dN}}{{dV}} = \dfrac{a}{{{V_0}}}V$
Now, we can rewrite this as, $dN = \dfrac{a}{{{V_0}}}VdV$
Integrating over the limit for $N$ $0 \to N$ and for $V$ $0 \to {V_0}$ we have,
$\int\limits_0^N {dN} = \dfrac{a}{{{V_0}}}\int\limits_0^{{V_0}} {VdV}$
Putting the value of the limit we have,
$N = \dfrac{a}{{{V_0}}}\dfrac{{{V_0}^2}}{2}$
Up on simplifying we have, $N = \dfrac{{a{V_0}}}{2}$
So, we can see, $2N = a{V_0}$
Hence, the value of $a{V_0}$ is $2N$

Hence, option A is the correct answer.

Note: The r.m.s value of $V$ is ${V_{rms}} = \dfrac{1}{N}\int\limits_0^{{V_0}} {{V^2}dN}$ which is equal to the $\sqrt {\dfrac{{a{V_0}^3}}{{4N}}}$ and the average value of $V$ is ${V_{avg}} = \dfrac{1}{N}\int\limits_0^{{V_0}} {VdN}$ which is equal to the value $\dfrac{{a{V_0}^2}}{{3N}}$. Hence, all the options except option (A) are incorrect. You can perform the integration by yourself to check the answers for further insight.