Solveeit Logo
Login

Question

Question: Graph of $y = P(x) = ax^5 + bx^4 + cx^3 + dx^2 + ex + f$, is given Question: If $P''(x) = 0$ has r...

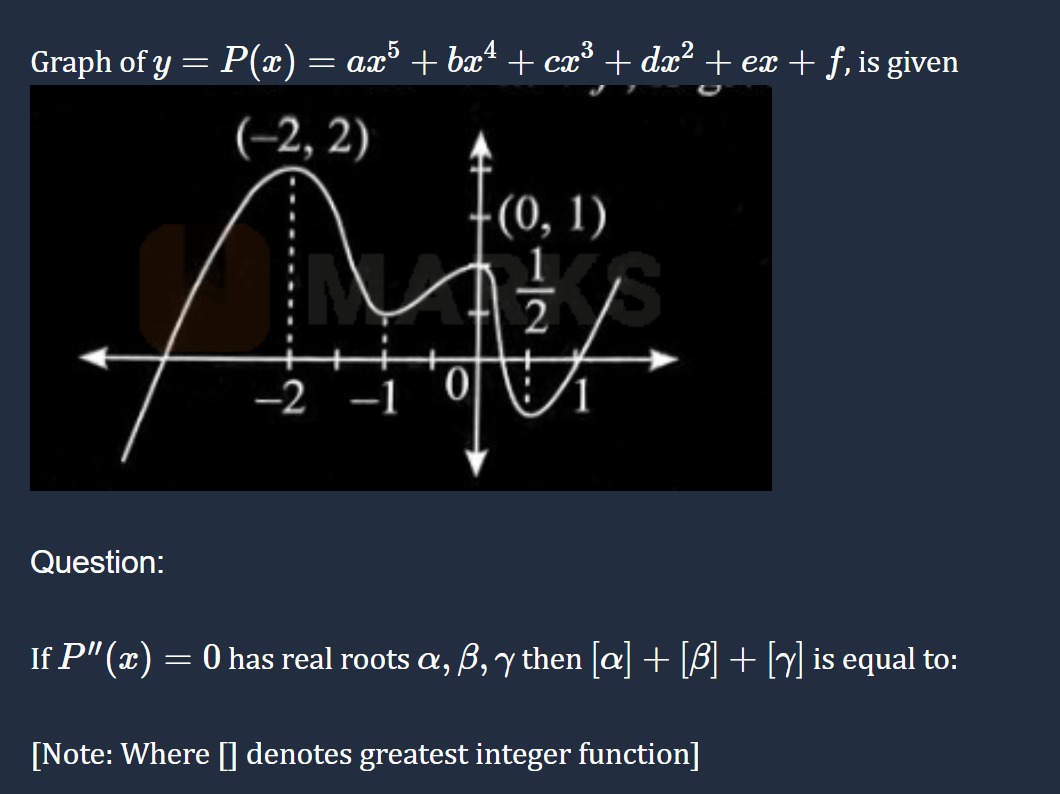
Graph of y=P(x)=ax5+bx4+cx3+dx2+ex+fy = P(x) = ax^5 + bx^4 + cx^3 + dx^2 + ex + f, is given

Question:

If P′′(x)=0P''(x) = 0 has real roots α,β,γ\alpha, \beta, \gamma then [α]+[β]+[γ][\alpha] + [\beta] + [\gamma] is equal to:

[Note: Where [] denotes greatest integer function]

A

5

B

-5

C

4

D

-4

Answer

-5

Explanation

Solution

The roots of P′′(x)=0P''(x) = 0 are the inflection points of the graph of y=P(x)y = P(x). An inflection point is where the concavity of the graph changes.

From the graph, we observe the changes in concavity:

  1. For xx far to the left, the graph is concave down (bending downwards).
  2. The concavity changes from concave down to concave up somewhere before the local maximum at x=−2x=-2. Let this inflection point be α\alpha. From the graph, α\alpha appears to be between −3-3 and −2-2. A rough estimate might be around −2.5-2.5. So, −3<α<−2-3 < \alpha < -2.
  3. The concavity changes from concave up to concave down somewhere between the local maximum at x=−2x=-2 and the local minimum at x=0x=0. Let this inflection point be β\beta. From the graph, β\beta appears to be between −1-1 and 00. A rough estimate might be around −0.5-0.5. So, −1<β<0-1 < \beta < 0.
  4. The concavity changes from concave down to concave up somewhere after the local minimum at x=0x=0. Let this inflection point be γ\gamma. From the graph, γ\gamma appears to be between 00 and 11. A rough estimate might be around 0.50.5. So, 0<γ<10 < \gamma < 1.

We are given that P′′(x)=0P''(x) = 0 has real roots α,β,γ\alpha, \beta, \gamma. These are the x-coordinates of the inflection points. From our observation of the graph, the approximate locations of the inflection points are in the intervals (−3,−2)(-3, -2), (−1,0)(-1, 0), and (0,1)(0, 1).

Based on these estimated intervals:

  • If −3<α<−2-3 < \alpha < -2, then [α]=−3[\alpha] = -3.
  • If −2<β<0-2 < \beta < 0, then [β]=−2[\beta] = -2 or −1-1.
  • If 0<γ<10 < \gamma < 1, then [γ]=0[\gamma] = 0.

So, with the estimated intervals:

  • −3<α<−2  ⟹  [α]=−3-3 < \alpha < -2 \implies [\alpha] = -3
  • −2<β<−1  ⟹  [β]=−2-2 < \beta < -1 \implies [\beta] = -2
  • 0<γ<1  ⟹  [γ]=00 < \gamma < 1 \implies [\gamma] = 0

Then [α]+[β]+[γ]=−3+(−2)+0=−5[\alpha] + [\beta] + [\gamma] = -3 + (-2) + 0 = -5.