Question

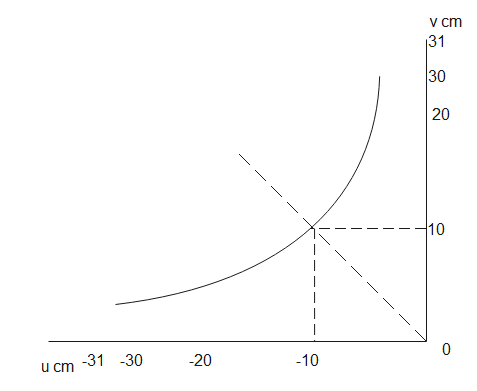
Graph of position of image versus position of point object from a convex lens is shown. Then, focal length of the lens is

A. $0.50 \pm 0.05{\text{ cm}}$
B. $5.00 \pm 0.05{\text{ cm}}$
C. $0.50 \pm 0.10{\text{ cm}}$
D. $5.00 \pm 0.10{\text{ cm}}$

Answer 1

Lens are the things which will allow the light to pass through them with convergence or divergence. Depending on whether the lens will converge or diverge the rays they are divided into convex and concave lenses. Their capacity of convergence or divergence is given by power of the lens. We have a lens equation to find out the position where the image is formed.

Formula used: $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$

Complete step by step answer:
When an object is placed in front of the lens the rays from the object passes through the lens and suffers refraction and image is formed. The position where image forms and the nature of the image formed depends upon the type of lens we use.
Various positions of placing an object in front of a convex lens gives us various positions of images.
If an object is placed between the pole and focus of the convex lens then image will be formed on the same side of the lens. That image formed can be enlarged and virtual and erect and on the other side.
Now if we place an object between focus and center then the image is formed away from the center and the image will be real and inverted. The size of the image will be bigger than an object.
For concave lenses there is always a diminished virtual image formed on the same side of the lens.
Applying lens equation for convex lens
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where ‘u’ is object distance and ‘v’ is the image distance and ‘f’ is focal length

From the above diagram it is clearly evident that if u=-10cm the v is 10cm.
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
\eqalign{ & \Rightarrow \dfrac{1}{{10}} - \dfrac{1}{{( - 10)}} = \dfrac{1}{f} \cr & \Rightarrow \dfrac{2}{{10}} = \dfrac{1}{f} \cr & \Rightarrow \dfrac{1}{5} = \dfrac{1}{f} \cr & \therefore f = 5cm \cr}
The least count of the measurement scale in the above graph will be 0.1 cm, as between 30 and 31 cm there will be 10 divisions and the least value can be measured is 0.1cm.
From the lens equation if we differentiate we will get
\eqalign{ & \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f} \cr & \Rightarrow \dfrac{{\Delta f}}{{{f^2}}} = \dfrac{{\Delta u}}{{{u^2}}} + \dfrac{{\Delta v}}{{{v^2}}} \cr & \Rightarrow \dfrac{{\Delta f}}{{{f^2}}} = \dfrac{{0.1}}{{100}} + \dfrac{{0.1}}{{100}} \cr & \Rightarrow \Delta f = \left( {\dfrac{{0.1}}{{100}} + \dfrac{{0.1}}{{100}}} \right) \times 25 \cr & \therefore \Delta f = 0.05cm \cr}
So the focal length will be $f \pm \Delta f = 5.00 \pm 0.05{\text{ cm}}$

So, the correct answer is “Option B”.

Note: Concave mirror can be analogous to convex lens. All the properties of image formed by the concave mirror will be possessed by the image formed due to convex lens. The only difference between the two images will be the side where images are formed. If images are formed on the object side in a concave mirror then images will be formed on the other side of the convex lens. Rest everything will be the same for the same position of objects in both the cases. Same can be applied for convex mirrors and concave lenses.