Question

Graph $f\left( x \right) = {\left( {x + 1} \right)^2} - 4$ and its inverse?

Answer 1

First we have to find the inverse of the function by considering the given function as $y$, then swap the variables i.e., $x$ and $y$, then solve for $y$, then we have to find the coordinates that lie on both the functions , i.e., given function and the inverse of the function, then by plotting the points on the graph, we will get the required graph.

Complete step by step answer:
A graph is the picture of the points that make a function true. If $f$ is a function, then the inverse function, written ${f^{ - 1}}$, is a function such that ${f^{ - 1}}\left( {f\left( x \right)} \right)$ for all $x$. Inverse graphs have swapped domains and ranges. That is, the domain of the original function is the range of its inverse, and its range is the inverse's domain. Inverse functions' graphs are reflections over the line $y=x$.
The inverse function of $f\left( x \right)$ is written as ${f^{ - 1}}\left( x \right)$.
${f^{ - 1}}\left( {f\left( x \right)} \right) = x$and,
$f\left( {{f^{ - 1}}\left( x \right)} \right) = x$.
Given function is $f\left( x \right) = {\left( {x + 1} \right)^2} - 4$,
A function and its inverse will be symmetric around the line$y = x$, Switch the position of $x$and $y$ variables to find the inverse of a function.
We have, $y = f\left( x \right) = {\left( {x + 1} \right)^2} - 4$,
Now put some values for$x$,
Take$x = 1$,
$\Rightarrow y = {\left( {1 + 1} \right)^2} - 4$,
Now simplifying we get,
$\Rightarrow y = {\left( 2 \right)^2} - 4$,
Now again simplifying we get,
$\Rightarrow y = 4 - 4 = 0$,
So the point $\left( {1,0} \right)$lies on the graph of the given function.
Take$x = - 1$,
$\Rightarrow y = {\left( { - 1 + 1} \right)^2} - 4$,
Now simplifying we get,
$\Rightarrow y = {\left( 0 \right)^2} - 4$,
Now again simplifying we get,
$\Rightarrow y = 0 - 4 = - 4$,
So the point $\left( { - 1, - 4} \right)$lies on the graph of the given function.
Now graphing the given function, we get,

Now take the given function,
$\Rightarrow y = f\left( x \right) = {\left( {x + 1} \right)^2} - 4$,
Write the quadratic as $x = {\left( {y + 1} \right)^2} - 4$, after switching $x$and $y$positions.
Next, solve $x = {\left( {y + 1} \right)^2} - 4$, for $y$,
Now adding both sides with 4 we get,
$\Rightarrow x + 4 = {\left( {y + 1} \right)^2} - 4 + 4$,
Now simplifying we get,
$\Rightarrow x + 4 = {\left( {y + 1} \right)^2}$,
Now taking the square to the other side we get,
$\Rightarrow y + 1 = \pm \sqrt {x + 4}$,
Now subtracting 1 to both sides we get,
$\Rightarrow y + 1 - 1 = \pm \sqrt {x + 4} - 1$,
Now simplifying we get,
$\Rightarrow y = \pm \sqrt {x + 4} - 1$,
Take$x = - 4$,
$\Rightarrow y = \pm \sqrt { - 4 + 4} - 1$,
Now simplifying we get,
$\Rightarrow y = \pm \sqrt {\left( 0 \right)} - 1$,
Now again simplifying we get,
$\Rightarrow y = 0 - 1 = - 1$,
So the point $\left( { - 4, - 1} \right)$lies on the graph of the given function.
Take$x = 0$,
$\Rightarrow y = \pm \sqrt {0 + 4} - 1$,
Now simplifying we get,
$\Rightarrow y = \pm \sqrt 4 - 1$,
Now again simplifying we get,
$\Rightarrow y = \pm 2 - 1$,
If we take $y = 2 - 1 = 1$, and if we take $y = - 2 - 1 = - 3$
So the points $\left( {0,1} \right)$and $\left( {0, - 3} \right)$lies on the graph of the given function.
Now graphing the function we get,

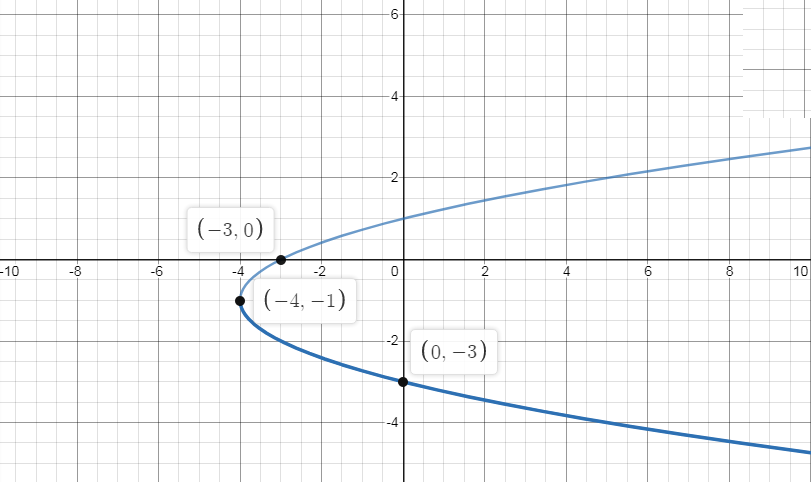
Now, graphing both the functions on the same graph we get,

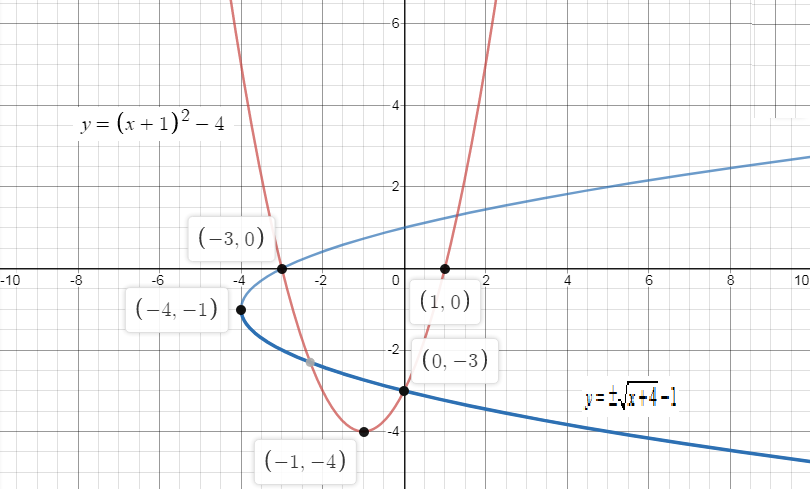
$\therefore$The graph of the$f\left( x \right) = {\left( {x + 1} \right)^2} - 4$ and its inverse is given by,

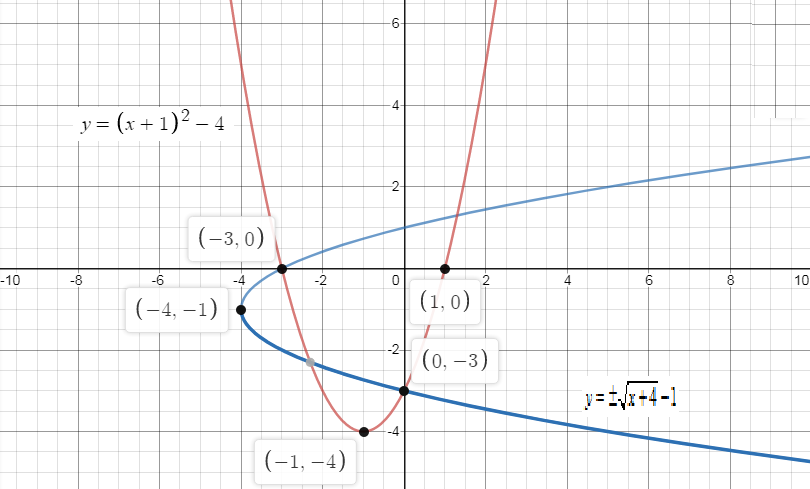
Note: When we graph the function and the inverse of the function on the same axis of the graph, the graph${f^{ - 1}}\left( x \right)$is the mirror reflection of the graph$f\left( x \right)$with respect to the line $y = x$.