Question

Graph $9{x^2} + 16{y^2} - 36x + 32y = 92$ algebraically.

Answer 1

Hint : Firstly, we will simplify the equation and after that we will find that the equation comes out is the general form of the equation of an ellipse and with the help of the equation we will form a graph, by finding its center, major axis and minor axis of the ellipse.

Formula used: The horizontal equation of the ellipse is,
$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - v} \right)}^2}}}{{{b^2}}} = 1$
Here $\left( {h,v} \right)$ is the center, $2a$ is the major axis and $2b$ is the minor axis.

Complete step by step solution:
The equation given in the problem is $9{x^2} + 16{y^2} - 36x + 32y = 92$ . Firstly, we will rearrange the equation, on rearranging, we get,
$$ $\Rightarrow 9{x^2} - 36x + 16{y^2} + 32y = 92$
Now, we will simplify the equation by taking some terms common,
$\Rightarrow 9\left( {{x^2} - 4x} \right) + 16\left( {{y^2} + 2y} \right) = 92$
Now, we will add and subtract $4$ in first parenthesis and we will add and subtract $1$ in second parenthesis,
$\Rightarrow 9\left( {{x^2} - 4x + 4 - 4} \right) + 16\left( {{y^2} + 2y + 1 - 1} \right) = 92$
Now, we will take $- 4$ out from the parenthesis, then it becomes $9 \times \left( { - 4} \right) = - 36$ and when we will take $- 1$ out from the parenthesis, then it becomes $16 \times \left( { - 1} \right) = - 16$ . Now, the equation will become,
$\Rightarrow 9\left( {{x^2} - 4x + 4} \right) - 36 + 16\left( {{y^2} + 2y + 1} \right) - 16 = 92$
Now, we will take $- 36$ and $- 16$ to the right side and then the equation becomes,
$\Rightarrow 9\left( {{x^2} - 4x + 4} \right) + 16\left( {{y^2} + 2y + 1} \right) = 92 + 36 + 16 \\\ \Rightarrow 9\left( {{x^2} - 4x + 4} \right) + 16\left( {{y^2} + 2y + 1} \right) = 144 \;$
Here, ${x^2} - 4x + 4$ is equal to ${\left( {x - 2} \right)^2}$ and ${y^2} + 2y + 1$ is equal to ${\left( {y + 1} \right)^2}$ , now we will substitute it in the above equation,
$\Rightarrow 9{\left( {x - 2} \right)^2} + 16{\left( {y + 1} \right)^2} = 144$
Now, we will divide the whole equation by $44$ , on dividing, we get,
$\Rightarrow \dfrac{{9{{\left( {x - 2} \right)}^2}}}{{144}} + \dfrac{{16{{\left( {y + 1} \right)}^2}}}{{144}} = \dfrac{{144}}{{144}}$
On further solving, we get,
$\Rightarrow \dfrac{{{{\left( {x - 2} \right)}^2}}}{{16}} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{9} = 1$
Now, we have an equation i.e, of an ellipse,
$\Rightarrow \dfrac{{{{\left( {x - 2} \right)}^2}}}{{{4^2}}} + \dfrac{{{{\left( {y - ( - 1)} \right)}^2}}}{{{3^2}}} = 1$
From the above formula, $\left( {2, - 1} \right)$ is the center of the ellipse and the major axis is $2 \times 4 = 8$ and the minor axis is $2 \times 3 = 6$ . Hence, the graph formed is,

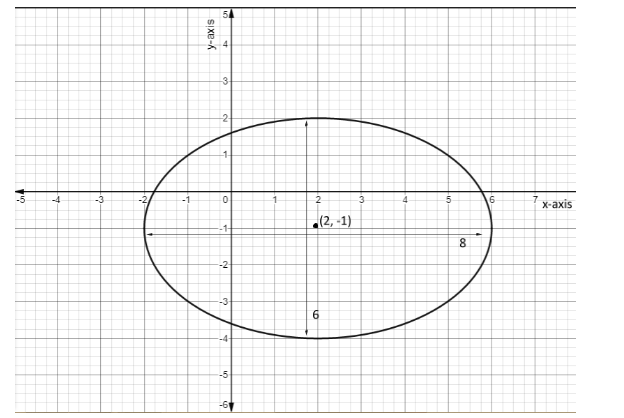
Note : When a set of points on a plane forms an oval, curved shape then it is called an ellipse. The equation formed of an ellipse above has the number $4$ that is greater than $3$ and is under x, then the ellipse formed is horizontal and if the greater number is under y, then the ellipse formed is vertical.