Question

$g(n) = \int_0^{n^2+n+1} e^{x/2-\lfloor x/2 \rfloor}(\frac{x}{2}-\lfloor\frac{x}{2}\rfloor)d(x-\lfloor x\rfloor); n \in N \text{ then } g(n)$

Answer 1

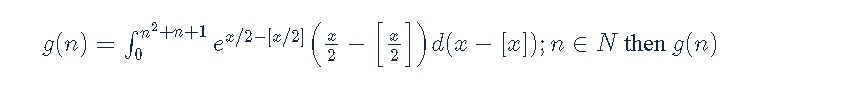
g(n)=n^2+n+2-e^{\frac{1}{2}}.

Answer 2

We start with

$$g(n)=\int_0^{n^2+n+1} e^{x/2-\lfloor x/2 \rfloor}\Bigl(\frac{x}{2}-\lfloor x/2 \rfloor\Bigr)d\Bigl(x-\lfloor x\rfloor\Bigr),$$

where we note that for any real number $x$,

$$\frac{x}{2}-\lfloor x/2\rfloor=\{x/2\},\quad \text{and} \quad x-\lfloor x\rfloor=\{x\}.$$

Thus, the integral becomes

$$g(n)=\int_0^{n^2+n+1} e^{\{x/2\}}\,\{x/2\}\;d\{x\}.$$

Step 1. Partitioning the integral

Since the fractional part $\{x\}$ resets at every integer, we split the integration interval $[0, n^2+n+1]$ into unit intervals. Write $x=m+s$ where $m=\lfloor x\rfloor$ (an integer) and $s=\{x\}\in[0,1)$. On each interval, $dx=d s$ (because away from the jump points, $d\{x\}=ds$).

Step 2. Behavior of $\{x/2\}$ based on parity of $m$

Write

$$\frac{x}{2}=\frac{m+s}{2}=\frac{m}{2}+\frac{s}{2}.$$

The floor of $\frac{x}{2}$ depends on whether $m$ is even or odd.

• Case 1: $m=2k$ (even).
  Then,

  $$\frac{x}{2}= k+\frac{s}{2}\quad\Rightarrow\quad \lfloor x/2\rfloor =k,$$

  so that

  $$\{x/2\}=\frac{s}{2}.$$

• Case 2: $m=2k+1$ (odd).
  Then,

  $$\frac{x}{2}= k+\frac{1}{2}+\frac{s}{2}\quad\Rightarrow\quad \lfloor x/2\rfloor = k,$$

  because $\frac{1}{2}+\frac{s}{2}\in[0.5,1)$ for $s\in[0,1)$. Hence,

  $$\{x/2\}=\frac{1}{2}+\frac{s}{2}=\frac{1+s}{2}.$$

Let $I_{\text{even}}$ be the integral over one unit interval for even $m$ and $I_{\text{odd}}$ for odd $m$:

$$I_{\text{even}}=\int_0^1 e^{\frac{s}{2}}\left(\frac{s}{2}\right)ds,\quad I_{\text{odd}}=\int_0^1 e^{\frac{1+s}{2}}\left(\frac{1+s}{2}\right)ds.$$

Step 3. Calculating $I_{\text{even}}$

Write

$$I_{\text{even}}=\frac{1}{2}\int_0^1 s\,e^{s/2}ds.$$

Use integration by parts: Let $u=s$ so that $du=ds$ and $dv=e^{s/2}ds$ with $v=2e^{s/2}$. Then,

$$\int s\,e^{s/2}ds = 2s\,e^{s/2} - \int 2e^{s/2}ds=2s\,e^{s/2} - 4e^{s/2}+C.$$

Evaluating from $0$ to $1$:

$$\int_0^1 s\,e^{s/2}ds = \Bigl[2e^{1/2}-4e^{1/2}+4\Bigr]-[0-4+4]= -2e^{1/2}+4.$$

Thus,

$$I_{\text{even}}=\frac{1}{2}(-2e^{1/2}+4)=2-e^{1/2}.$$

Step 4. Calculating $I_{\text{odd}}$

We have

$$I_{\text{odd}}=\frac{1}{2}\int_0^1 e^{\frac{1+s}{2}}(1+s)ds.$$

Factor out $e^{1/2}$:

$$I_{\text{odd}}=\frac{e^{1/2}}{2}\int_0^1 (1+s)e^{s/2}ds.$$

Let

$$J=\int_0^1 (1+s)e^{s/2}ds = \int_0^1 e^{s/2}ds + \int_0^1 s\,e^{s/2}ds.$$

First,

$$\int_0^1 e^{s/2}ds=2(e^{1/2}-1).$$

We already found $\int_0^1 s\,e^{s/2}ds= -2e^{1/2}+4$. Thus,

$$J=2(e^{1/2}-1) + (-2e^{1/2}+4)=2.$$

It follows that

$$I_{\text{odd}}=\frac{e^{1/2}}{2}\cdot 2=e^{1/2}.$$

Step 5. Summing up over all intervals

The integration variable $x$ goes from $0$ to $n^2+n+1$. There are

$$M=n^2+n+1$$

unit intervals and the integration is a sum over these. Since the measure is $ds$ on each unit interval, we only add contributions on each full interval. In the range $0,1,2,\dots, M-1$, the number of even integers is $\frac{M+1}{2}$ and odd integers is $\frac{M-1}{2}$ (since $M$ is odd because $n(n+1)$ is even).

Thus,

$$g(n)=\frac{M+1}{2}I_{\text{even}}+\frac{M-1}{2}I_{\text{odd}},$$

with $I_{\text{even}}=2-e^{1/2}$ and $I_{\text{odd}}=e^{1/2}$. Substitute:

$$g(n)=\frac{M+1}{2}(2-e^{1/2})+\frac{M-1}{2}e^{1/2}.$$

Simplify:

$$g(n)=\frac{1}{2}\Bigl[(M+1)(2-e^{1/2})+(M-1)e^{1/2}\Bigr].$$

Expanding,

$$(M+1)(2-e^{1/2})=2M+2 - M e^{1/2} - e^{1/2},$$ $$(M-1)e^{1/2}=M e^{1/2}- e^{1/2}.$$

Adding these:

$$2M+2 - M e^{1/2} - e^{1/2} + M e^{1/2}- e^{1/2}=2M+2-2e^{1/2}.$$

Thus,

$$g(n)=\frac{1}{2}[2M+2-2e^{1/2}]=M+1-e^{1/2}.$$

Recalling $M=n^2+n+1$, we obtain:

$$g(n)=n^2+n+1+1-e^{1/2}=n^2+n+2-e^{1/2}.$$