Question

Globular proteins are present in :
(A) blood
(B) keratin
(C) muscles
(D) none of these

Answer 1

Packing efficiency can be defined as the percentage of space obtained by constituent particles that are packed within the lattice.
In a body centered cubic unit cell, one atom is located at the body center apart from corners of the cube.

Complete step by step answer:
Step by step solution:
In a body-centered cubic unit cell atoms are present at the corners of the unit cell and one atom occupies the center of the unit cell.
Packing Efficiency $= \dfrac{{Volume\;occupied\;by\;the\;atom\operatorname{s} \;in\;a\;unit\;cell}}{{Total\;volume\;of\;unit\;cell}} \times 100$
The relationship between the radius r and the edge length of a unit cell is given as
$a = \dfrac{{4r}}{{\sqrt 3 }}$
To find the volume of a unit cell we increase edge length by three-time
${a^3} = {\left( {\dfrac{{4r}}{{\sqrt 3 }}} \right)^3} = \dfrac{{64{r^3}}}{{3\sqrt 3 }}$
The number of atoms per unit cell in a body-centered cell is 2.
The volume of a sphere is $= \dfrac{4}{3}\pi {r^3}$
Volume of each unit cell $= 2 \times \dfrac{4}{3}\pi {r^3} = \dfrac{8}{3}\pi {r^3}$
Substituting the values in the above equation
Packing Efficiency $= \dfrac{{\dfrac{8}{3}\pi {r^3}}}{{\dfrac{{64{r^3}}}{{3\sqrt 3 }}}} \times 100 = 68.04$
The packing efficiency of Body-Centered Cubic lattice is equal to $68.04\%$.
In a body-centered cubic structure, the space occupied is about the concept: Packing efficiency – Efficiency of packing in body-centered cubic structures.

So, the correct answer is Option A.

Note: Alternative method: There is an alternate method to find the packing efficiency of Body-Centered Cubic Lattice as follows:

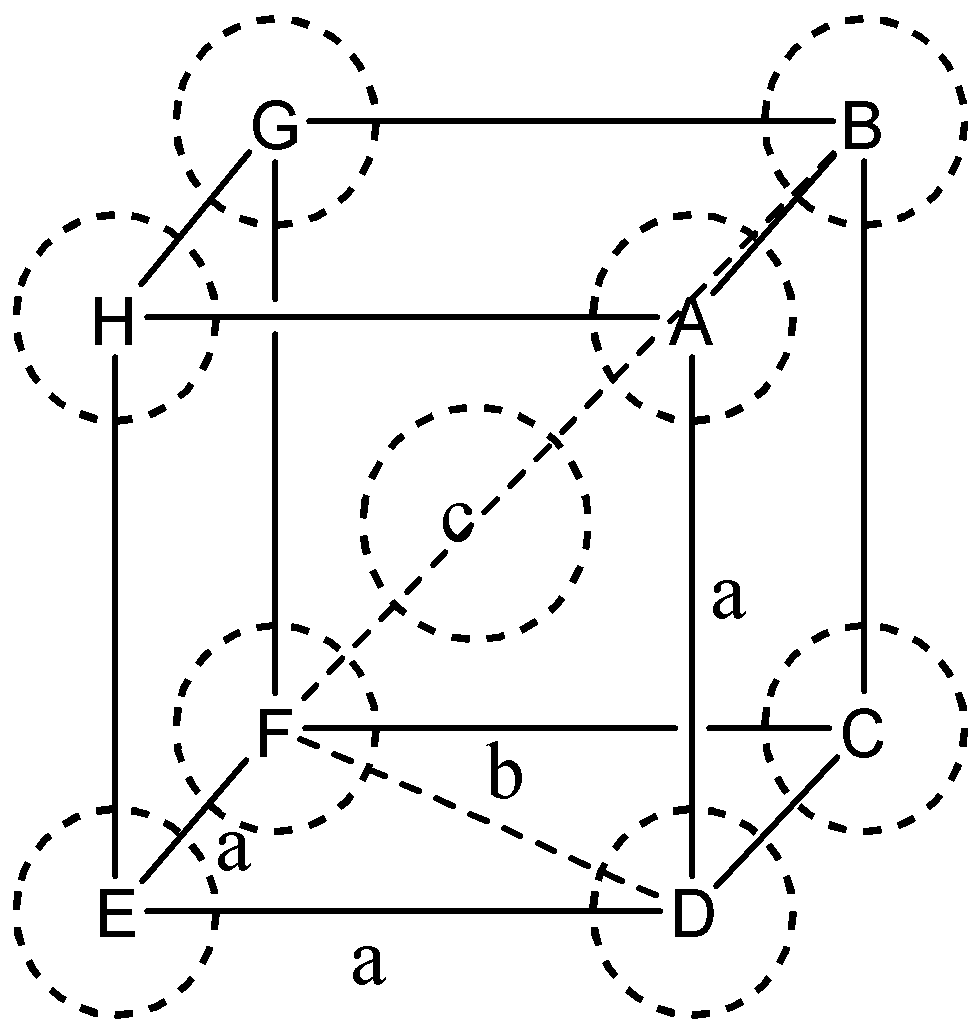
In the body-centered cubic unit cell
$\Rightarrow$ In $\Delta EFD$
$\Rightarrow$ Let $DF = b$
and we know $ED = EF = a$ (edge length)
Now,
${b^2} = {a^2} + {a^2} = 2{a^2}$
In $\Delta AFD$
Let, $AF = c$
We know that$FD = b$ and $AD = a$ (edge length)
Now,
${c^2} = {a^2} + {b^2} = {a^2} + 2{a^2} = 2{a^2}$
Or $c = \sqrt 3 a$
We know that c is body diagonal. As the sphere at the center touches the sphere at the corner. Therefore body diagonal $c = 4$
$\Rightarrow \sqrt 3 a = 4r$
$\Rightarrow r = \left( {\dfrac{{\sqrt 3 }}{4}} \right)a$
$\Rightarrow a = \dfrac{{4r}}{{\sqrt 3 }}$
Volume of the unit cell ${a^3} = {\left( {\dfrac{{4r}}{{\sqrt 3 }}} \right)^3} = \dfrac{{64{r^3}}}{{3\sqrt 3 }}$
No. of spheres in bcc $= 2$
Volume of 2 spheres $= 2 \times \dfrac{4}{{3\pi {r^3}}}$
$Packing.Efficiency = \dfrac{{Volume\;occupied\;by\;two\;sphere\operatorname{s} \;in\;the\;unit\;cell \times 100}}{{Total\;volume\;of\;the\;unit\;cell}}\%$
$= \dfrac{{2 \times \left( {\dfrac{4}{3}} \right)\pi {r^3} \times 100}}{{{{\left[ {\left( {\dfrac{4}{{\sqrt 3 }}} \right)r} \right]}^3}}}\%$
$= \dfrac{{\left( {\dfrac{8}{3}} \right)\pi {r^3} \times 100}}{{\dfrac{{64}}{{\left( {3\sqrt 3 } \right)}}{r^3}}}\%$
$= 68\%$
The packing efficiency for body centered cubic lattice is $68\%$