Question

Given $y=-2{{\left( x+4 \right)}^{2}}-3$, how do you find the vertex and axis of symmetry?

Answer 1

From the question we have been asked to find the vertex and axis of symmetry of a parabola. To solve this question, we will use the formula of standard form parabola in vertex form which is $y=a{{\left( x-h \right)}^{2}}+k$. Here in this standard form $(h,k)$ is the vertex. For finding the axis of symmetry of the parabola we will use the principle which is “the axis of symmetry passes through the vertex”. In this way we will find the solution to the given question.

Complete step-by-step answer:
So, firstly from the basic formula for the standard form of parabola in vertex form is $y=a{{\left( x-h \right)}^{2}}+k$.
Here in this form the coordinates of the vertex are $(h,k)$.
Now, we will reduce the given parabola equation into the standard form. So, the equation will be simplified as follows.
$\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$
$\Rightarrow y=-2{{\left( x+4 \right)}^{2}}-3$
$\Rightarrow y=\left( -2 \right){{(x-(-4))}^{2}}+(-3)$
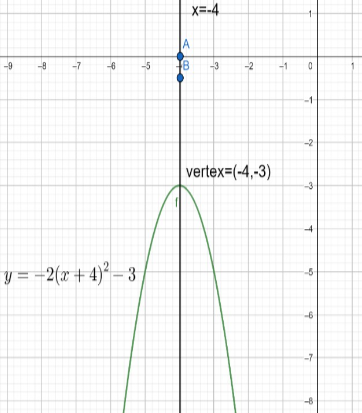
Now, we compare the reduced equation with standard form of parabola. We get, $h=-4$ and $k=-3$.
So, the vertex $(h,k)$ will be as follows.
$\Rightarrow (h,k)=\left( -4,-3 \right)$
Now, we know that for a parabola the axis of symmetry passes through the vertex of the parabola.
Since the coefficient of ${{\left( x+4 \right)}^{2}}$ is $-2$ the parabola opens downwards.
So, the equation of axis of symmetry is as follows.
$\Rightarrow x=h$
$\Rightarrow x=-4$

Note: Students must not do any calculation mistakes. Students must not have good knowledge in the concept of parabola and its formulae.
Students should know the vertex form of parabola which is $\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$. Students should not be confused that for this vertex form the vertex will be $(h,k)$ if and only if the given question is converted into $\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$ form or else our solution will be wrong.