Question

Given vector A: 25.2 cm at 81.6 degrees and vector B: 32.1 cm at 142.7 degrees. How do you add and subtract these two vectors?

Answer 1

As it is clear from the question that we need to find the resultant of the addition and subtraction of two vectors so, for that we are going to apply here, ${{A}_{x}}=\text{length of A }\cos \left( \text{degree of A} \right),{{A}_{y}}=\text{length of A }\sin \left( \text{degree of A} \right)$, ${{B}_{x}}=\text{length of B }\cos \left( \text{degree of B} \right),{{B}_{y}}=\text{length of B }\sin \left( \text{degree of B} \right)$. Also, we will use the formula $\vec{A}+\vec{B}=\sqrt{{{\left( {{{\vec{A}}}_{x}}+{{{\vec{B}}}_{x}} \right)}^{2}}+{{\left( {{{\vec{A}}}_{y}}+{{{\vec{B}}}_{y}} \right)}^{2}}},\vec{A}-\vec{B}=\sqrt{{{\left( {{{\vec{A}}}_{x}}-{{{\vec{B}}}_{x}} \right)}^{2}}-{{\left( {{{\vec{A}}}_{y}}-{{{\vec{B}}}_{y}} \right)}^{2}}}$ to get the right answer.

Complete step-by-step answer:
Two dimensional vector additions: In this type of addition two vectors participate in this process. The two vectors can be any vectors but when they are added together, which results into their addition as shown in the following diagram.

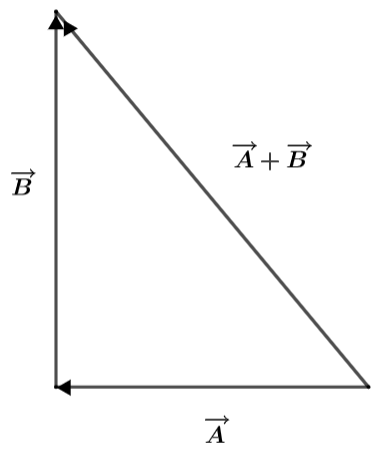
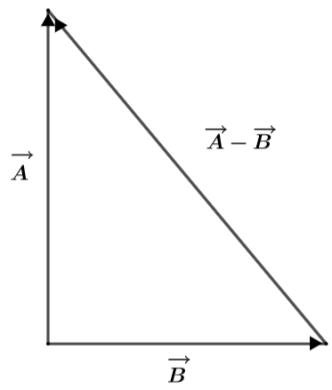
Two dimensional vector subtractions: In this type of subtraction two vectors participate in this process also. The two vectors can be any vectors but here they are subtracted together. This can be understood from the following diagram.

According to the question we have got two vectors. These two vectors along with their proper dimensions are shown in the figure below.

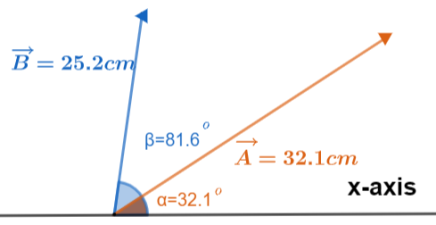
As there are two components of any vector so, we have that the given vectors will also have two components namely, sine component (representing y component) and cosine component (representing x component). We will first consider vector A and write its rectangular components as ${{A}_{x}}=\text{length }\cos \left( \text{degree} \right),{{A}_{y}}=\text{length }\sin \left( \text{degree} \right)$. Since, the length of vector A is 25.2 cm and degree is 81.6 degrees therefore, we have

& {{A}_{x}}=25.2\cos \left( 81.6 \right),{{A}_{y}}=25.2\sin \left( 81.6 \right) \\\ & \Rightarrow {{A}_{x}}=25.2\times 0.146,{{A}_{y}}=25.2\times 0.989 \\\ & \Rightarrow {{A}_{x}}=3.6792,{{A}_{y}}=24.9228 \\\ & \approx {{A}_{x}}=3.67,{{A}_{y}}=24.92 \\\ \end{aligned}$$ Similarly, we get components off B as, $$\begin{aligned} & {{B}_{x}}=32.1\cos \left( 142.7 \right),{{B}_{y}}=32.1\sin \left( 142.7 \right) \\\ & \Rightarrow {{B}_{x}}=32.1\times -0.7954,{{B}_{y}}=32.1\times 0.6059 \\\ & \Rightarrow {{B}_{x}}=-25.53,{{B}_{y}}=19.449 \\\ & \approx {{B}_{x}}=-25.53,{{B}_{y}}=19.45 \\\ \end{aligned}$$ In case of vector addition the vectors will be like the following diagram.  Therefore, we will add the two vectors by adding their components. This gives us, $$\begin{aligned} & \vec{A}+\vec{B}=\sqrt{{{\left( {{{\vec{A}}}_{x}}+{{{\vec{B}}}_{x}} \right)}^{2}}+{{\left( {{{\vec{A}}}_{y}}+{{{\vec{B}}}_{y}} \right)}^{2}}} \\\ & \Rightarrow \vec{A}+\vec{B}=\sqrt{{{\left( 3.67-25.53 \right)}^{2}}+{{\left( 24.92+19.45 \right)}^{2}}} \\\ & \Rightarrow \vec{A}+\vec{B}=\sqrt{{{\left( -21.86 \right)}^{2}}+{{\left( 44.37 \right)}^{2}}} \\\ & \Rightarrow \vec{A}+\vec{B}=\sqrt{477.8596+1968.6969} \\\ & \Rightarrow \vec{A}+\vec{B}=\sqrt{2446.5565}=49.4626 \\\ & \Rightarrow \vec{A}+\vec{B}\approx 49.46 \\\ \end{aligned}$$ Similarly, the subtraction of these vectors on the basis of their components will results into,  $$\begin{aligned} & \vec{A}-\vec{B}=\sqrt{{{\left( {{{\vec{A}}}_{x}}-{{{\vec{B}}}_{x}} \right)}^{2}}-{{\left( {{{\vec{A}}}_{y}}-{{{\vec{B}}}_{y}} \right)}^{2}}} \\\ & \Rightarrow \vec{A}-\vec{B}=\sqrt{{{\left( 3.67-\left( -25.53 \right) \right)}^{2}}-{{\left( 24.92-19.45 \right)}^{2}}} \\\ & \Rightarrow \vec{A}-\vec{B}=\sqrt{{{\left( 3.67+25.53 \right)}^{2}}-{{\left( 24.92-19.45 \right)}^{2}}} \\\ & \Rightarrow \vec{A}-\vec{B}=\sqrt{{{\left( 29.2 \right)}^{2}}-{{\left( 5.47 \right)}^{2}}} \\\ & \Rightarrow \vec{A}-\vec{B}=\sqrt{852.64-29.9209} \\\ & \Rightarrow \vec{A}-\vec{B}=\sqrt{822.7191} \\\ & \Rightarrow \vec{A}-\vec{B}=28.6830 \\\ & \Rightarrow \vec{A}-\vec{B}\approx 28.68 \\\ \end{aligned}$$ Hence, the addition of these two vectors is 49.46 and the subtraction is 28.68. **Note:** Vectors can be very tricky if not focused while solving them. Since, there are two vectors, we will first draw their diagram along with their given dimensions. After this for getting their resultant of addition and subtraction of two vectors, we should focus on the arrow of vectors. With the help of these arrows we can create the right resultant vector. While adding the two vectors we should not forget about taking the root, after adding the squares of components of two vectors. Focus is most important while solving the question otherwise; we might get a wrong answer which of course, is not needed here.