Question

Given two functions $f\left( x \right)\text{ and }g\left( x \right)$ . For what x does the equation $f'\left( x \right)=g\left( x \right)$ hold true?
$f\left( x \right)={{\sin }^{3}}2x$ and $g\left( x \right)=4\cos 2x-5\sin 4x$ .

Answer 1

Start by finding the derivative of x using chain rule of differentiation followed by substituting it along with g(x) in $f'\left( x \right)=g\left( x \right)$ . Use the formula that $\sin 4x=2\cos 2x\sin 2x$ and take cos2x common from the right hand side. Cancel cos2x from both sides and solve the quadratic equation to get the values of x. Remember that the general solution of sinx=siny is $x=n\pi +{{\left( -1 \right)}^{n}}y$ and of cosx=cosy is $x=2n\pi \pm y$.

Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sin x.

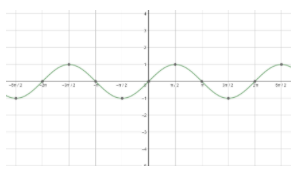
Next, let us see the graph of cos x.

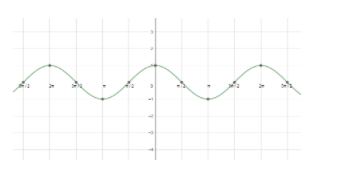
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ$
Now let us start the solution to the above question by finding the derivative of f(x).
$f\left( x \right)={{\sin }^{3}}2x$
Applying chain rule of differentiation and using the formula $\dfrac{d\left( \sin x \right)}{dx}=\cos xdx$ , we get
$f'\left( x \right)=3\times 2\times {{\sin }^{2}}2x\times \cos 2x=6{{\sin }^{2}}2x\cos 2x$
Now we will start solving the equation $f'\left( x \right)=g\left( x \right)$ .
$6{{\sin }^{2}}2x\cos 2x=4\cos 2x-5\sin 4x$
We know that $\sin 4x=2\cos 2x\sin 2x$ . So, using this in our equation, we get
$6{{\sin }^{2}}2x\cos 2x=4\cos 2x-5\times 2\sin 2x\cos 2x$
$\Rightarrow 6{{\sin }^{2}}2x\cos 2x=\left( 2-5\sin 2x \right)\times 2\cos 2x$
Now we will cancel cos2x from both sides. But if cos2x is zero, both sides become zero, so, one of the solutions to the above equation is cos2x= 0 and we know that $\cos \dfrac{\pi }{2}=0$ .
$\therefore \cos \dfrac{\pi }{2}=\cos 2x$
We know that the general solution of cosx=cosy is $x=2n\pi \pm y$ .
$\therefore 2x=2n\pi \pm \dfrac{\pi }{2}$
$\Rightarrow x=n\pi \pm \dfrac{\pi }{4}$
Now let us again move to the parent equation and consider the case when cos2x is not equal to 0.
$6{{\sin }^{2}}2x\cos 2x=\left( 2-5\sin 2x \right)\times 2\cos 2x$
$\Rightarrow 3{{\sin }^{2}}2x=2-5\sin 2x$
$\Rightarrow 3{{\sin }^{2}}2x+5\sin 2x-2=0$
So, the equation is a quadratic equation in sin2x. So, we can write 5 as 6-1. On doing so, we get
$3{{\sin }^{2}}2x+6\sin 2x-\sin 2x-2=0$
$\Rightarrow 3\sin 2x\left( \sin 2x+2 \right)-1\left( \sin 2x+2 \right)=0$
$\Rightarrow \left( 3\sin 2x-1 \right)\left( \sin 2x+2 \right)=0$
Now the factor (sin2x+2) is of no use, as sine cannot have a value of -2 as it is always greater than -1. So, let us solve the other factor.
$3\sin 2x-1=0$
$\Rightarrow \sin 2x=\dfrac{1}{3}$
Now this can be written as:
$\sin 2x=\sin \left( {{\sin }^{-1}}\dfrac{1}{3} \right)$
We know that the general solution of sinx=siny is $x=n\pi +{{\left( -1 \right)}^{n}}y$ .
$\therefore 2x=n\pi +{{\left( -1 \right)}^{n}}{{\sin }^{-1}}\dfrac{1}{3}$
$\Rightarrow x=\dfrac{n\pi }{2}+\dfrac{{{\left( -1 \right)}^{n}}}{2}{{\sin }^{-1}}\dfrac{1}{3}$
So, the solutions to the above question is $x=n\pi \pm \dfrac{\pi }{4}$ and $x=\dfrac{n\pi }{2}+\dfrac{{{\left( -1 \right)}^{n}}}{2}{{\sin }^{-1}}\dfrac{1}{3}$ , where n can be any integer number.

Note: Be careful about the calculation and the signs of the formulas you use as the signs in the formulas are very confusing and are very important for solving the problems. Also, remember that $\dfrac{1}{3}=\sin \left( {{\sin }^{-1}}\dfrac{1}{3} \right)$ is a complete result but $2x={{\sin }^{-1}}\left( \sin 2x \right)$ is not always correct. Also, don’t forget the solutions coming from the cos2x part, as it is cancelled.