Question

Given the vertical height of the projectile at time t is $y\text{ }=\text{ }4t\text{ }\text{- }5{{t}^{2}}$and the horizontal distance covered is given by $x\text{ }=\text{ }3t$. Then what is the angle of projection with the horizontal?
a) ${{\tan }^{-1}}\dfrac{3}{5}$
b) ${{\tan }^{-1}}\dfrac{4}{5}$
c) ${{\tan }^{-1}}\dfrac{4}{3}$
d) ${{\tan }^{-1}}\dfrac{3}{4}$

Answer 1

In order to solve this question, we first need to calculate velocity along the $x$ axis and $y$ axis. After that we will find the velocity of the projectile and then calculate the angle of projection.

Complete step-by-step solution:
let us draw the above problem to find the solution easily,

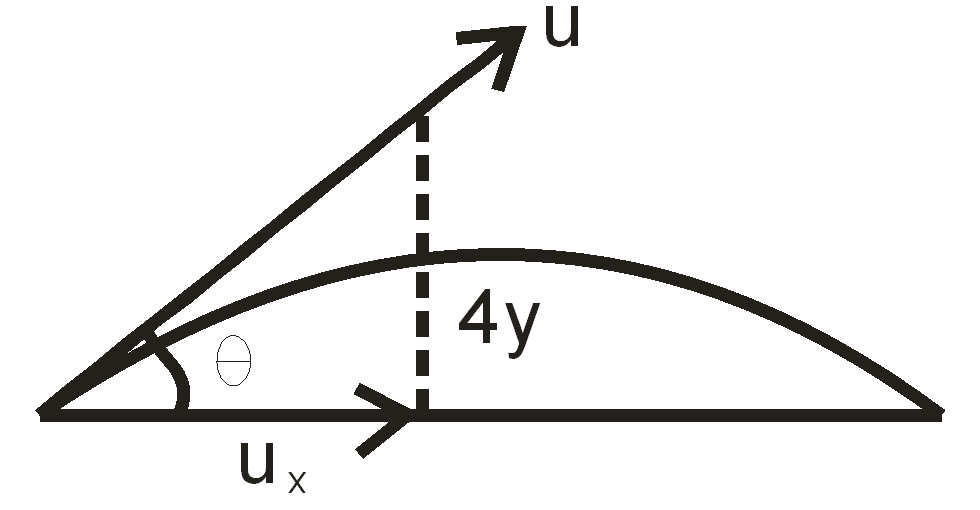
According to the question , we get
$y\text{ }=\text{ }4t\text{ }\text{-}5{{t}^{2}}$ and
$x\text{ }=\text{ }3t$
Now, we have to calculate the velocity along $x$- axis,
${{v}_{x}}\Rightarrow \dfrac{dx}{dt}\Rightarrow 3m/s$
Again , velocity along $y$- axis,
${{v}_{y}}\Rightarrow \dfrac{dy}{dt}$
${{v}_{y}}\Rightarrow 4-10t$
${{v}_{y}}_{t=0\sec}\Rightarrow 4m/s$
Therefore, velocity of the projectile,
$v\Rightarrow V_x\overrightarrow{i}+ V_y\overrightarrow{j}$
$v\Rightarrow \left( 3\overrightarrow{i}+4\overrightarrow{j} \right)m/s$
$\therefore$ Angle of projection,

& \tan \theta \Rightarrow \dfrac{V_y}{V_x} \\\ & \tan \theta \Rightarrow \dfrac{4}{3} \\\ & \theta \Rightarrow {{\tan }^{-1}}\left( \dfrac{4}{3} \right) \\\ \end{aligned}$$ **Therefore , option c is correct.** **Note:** Path of a projectile is known as trajectory, where range is known while the horizontal distance travels by the projectile. When the angle of projection is $${{45}^{\circ }}$$, the horizontal range becomes maximum .