Question

Given the measurements in the following figure: If $AD = m\sec \theta$ or $12\cos ec\theta$
Then, the value of $m$ is:

A.7
B.3
C.2
D.9

Answer 1

Here we need to find the value of the used variable. For that, we will first draw a perpendicular in the given figure such that we will get a rectangle. Then we will use the property of the rectangle and find the value of the unknown side. Then we will use the basic trigonometric formulas to get the final answer.

Complete step-by-step answer:
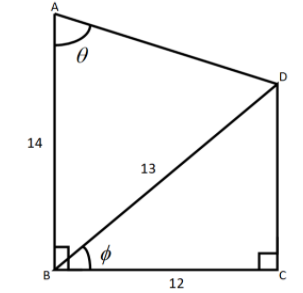
Here we have been given the quadrilateral.
We will first draw a perpendicular from point $D$ on side $AB$ and we will name that point of intersection as point $E$.

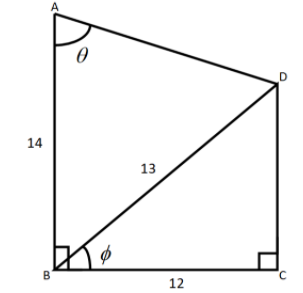
We can see that $\vartriangle BCD$ is a right angled triangle. So we will use the Pythagoras theorem here.
$B{D^2} = B{C^2} + C{D^2}$ ……….. $\left( 1 \right)$
As it is given that:-
BD = 13 \\\ BC = 12 \\\
Now, we will substitute all these values of sides in equation $\left( 1 \right)$. Therefore, we get
$\Rightarrow {13^2} = {12^2} + C{D^2}$
Applying the exponent on the terms, we get
$\Rightarrow 169 = 144 + C{D^2}$
Subtracting 144 from both the sides, we get
\Rightarrow 169 - 144 = 144 + C{D^2} - 144 \\\ \Rightarrow 25 = C{D^2} \\\
Now, taking square root on both sides of the equation, we get
\Rightarrow \sqrt {25} = \sqrt {C{D^2}} \\\ \Rightarrow 5 = CD \\\
Therefore, we get the value
$\Rightarrow CD = 5$
We can see that $BCDE$ is forming a rectangle as all the angles are equal to $90^\circ$.
We know that the opposite sides of the rectangle are equal to each other.
Therefore, using this property here, we get
$BE = CD = 5 \\\ BC = DE = 12 \\\$
Now, we will find the value of $AE$.
We know from figure that
$AE = AB - BE$
Now, substituting $AB = 14$ and $BE = 5$ in the above equation, we get
$\Rightarrow AE = 14 - 5$
On subtracting these numbers, we get
$\Rightarrow AE = 9$
We will again use the basic trigonometric formulas in $\vartriangle AED$.
We know from the trigonometric formulas $\cos \theta = \dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}}$.
Using this formula in $\vartriangle AED$, we get
$\cos \theta = \dfrac{{AE}}{{AD}}$
Now, substituting $AE = 9$ in the above equation, we get
$\Rightarrow \cos \theta = \dfrac{9}{{AD}}$
On cross multiplying the terms, we get
$\Rightarrow AD = \dfrac{{12}}{{\cos \theta }}$
We know from inverse trigonometric identities that $\sec \theta = \dfrac{1}{{\cos \theta }}$.
Therefore, using this identity here, we get
$\Rightarrow AD = 9\sec \theta$ ……….. $\left( 2 \right)$
But it is given that $AD = m\sec \theta$.
Now, we will compare this given value with the obtained equation $\left( 2 \right)$. Therefore, we get
$m = 9$
Therefore, the required value of $m$ is 9.
Hence, the correct option is option D.

Note: Here we have used the basic trigonometric identities and trigonometric formulas here. Trigonometric identities are defined as the equalities that are true only for the right angled triangles but if the triangle is not a right angled triangle then we can’t use trigonometric identities. Also we have used the Pythagoras theorem here which states that the square of the hypotenuse is equal to the sum of the square of the base and the height of the right angled triangle.