Question

Given the height of a kite is fixed at $40\,m$. The length of the string is $50\,m$ at a moment. Velocity of the kite in horizontal direction is $25\,m/sec$ at that time. Find the rate of slackening of the string at that time.

Answer 1

We know that velocity is a vector quantity and hence can be divided into components forces. The process of breaking a vector into its components is called resolving into components. Also we must draw the component forces perpendicular to each other. Following we have resolved the velocity vector into components to proceed further.

Complete step by step answer:

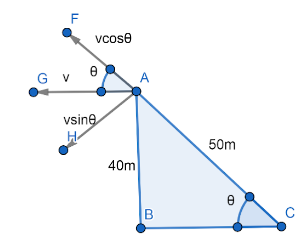
As we can see in the above diagram AB represents height of kite i.e. fixed at 40m. AC represents the length of the string at a moment i.e. 50m. Now since the velocity of the kite in horizontal direction is 25m/s, we resolve it into components. Here vcosθ represents the rate of slackening of the string at that time

Let us first find value of θ as follows
$\sin \theta = \dfrac{4}{5}$
Rearranging the terms we have
$\theta = {\sin ^{ - 1}}\dfrac{4}{5}$
We get value of $\theta = 53.1$
So rate of slackening of string is
$v\cos \theta = 25 \times \cos (53.1) \\\ \therefore v\cos \theta = 15\,m{s^{^{ - 1}}} \\\$
Therefore the rate of slackening of the string at that time will be $15\,m{s^{^{ - 1}}}$.

Note: Slacken means to loosen the tension on an object or tightness of something.Tension is generally described as the pulling force by means of a string, a cable, chain, or similar object. Tension is not a pushing force as ropes can’t push effectively.Attempting to push the rope will cause the rope to go slack, losing the tension it possesses. Tension is a force but it doesn’t cause any displacement.Therefore, the work done by tension is zero.