Question

Given the family of lines, $a(3x + 4y + 6) + b(x + y + 2) = 0$. The line of the family situated at the greatest distance from point $P\left( {2,3} \right)$ has an equation.
A) $4x + 3y + 8 = 0$
B) $5x + 3y + 10 = 0$
C) $15x + 8y + 30 = 0$
D) None of these

Answer 1

Initially we’ll notice the different equations from the family of equations of the line. Then we will find the intersection point.
From the graph, we can see that the perpendicular line passing through the intersection point will be at the greatest distance from the point $$$$$$\left( {2,3} \right)$$. So we’ll find that line’s equation to get our answer.

Complete step by step solution: Given, a family of line i.e. $a(3x + 4y + 6) + b(x + y + 2) = 0.$
A point $P(2,3)$.

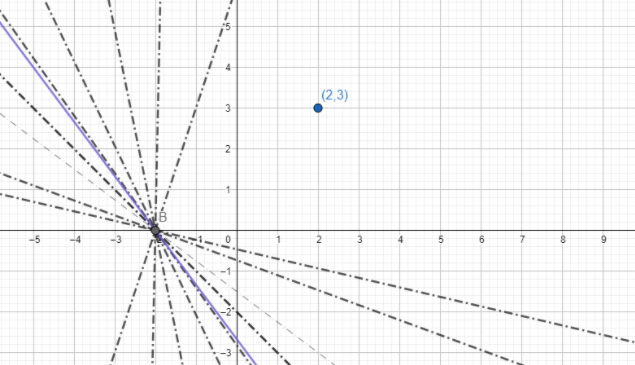
Now, From the family of lines given i.e., $a(3x + 4y + 6) + b(x + y + 2) = 0,$we get

$${l_1}{\text{ }}as{\text{ }}(3x + 4y + 6 = 0)........(i) \\\ {l_2}{\text{ }}as{\text{ }}(x + y + 2 = 0)............(ii) \\\$$

Substituting the value of ‘x’ from equation (ii) to equation(i), we get

$$3( - y - 2) + 4y + 6 = 0 \\\ \Rightarrow - 3y - 6 + 4y + 6 = 0 \\\ \Rightarrow y = 0 \\\$$

Now, putting the value of ‘y’ in equation(ii)

$$x + 0 + 2 = 0 \\\ \Rightarrow x = - 2 \\\$$

Therefore, the intersection point of ${l_1}{\text{ }}and{\text{ }}{l_2}$ is $\left( { - 2,0} \right)$
Equation of a line joining two points $({x_1},{y_1})$ and $({x_2},{y_2})$is given by
$(y - {y_1}) = \left( {\dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}} \right)(x - {x_1})$
Therefore, the equation of the line joining $\left( { - 2,0} \right)$ and$\left( {2,3} \right)$, the point from which the greatest distance is to be measured be ${{\text{l}}_{\text{3}}}$ i.e.,
$(y - 0) = \left( {\dfrac{{0 - 3}}{{ - 2 - 2}}} \right)(x + 2) \\\ \Rightarrow y = \dfrac{3}{4}(x + 2) \\\$
The slope of the line(${l_3}$) is $\dfrac{3}{4}$.
Now, the line perpendicular to the line ${l_3}$passing through the intersection of ${l_1}{\text{ }}and{\text{ }}{l_2}$i.e.,$\left( { - 2,0} \right)$ is the required line let be ${l_4}.$
The product of slopes of perpendicular lines is equal to(-1).

$$(slopes{\text{ }}of{\text{ }}{l_3})(slopes{\text{ }}of{\text{ }}{l_4}) = - 1 \\\ \dfrac{3}{4}(slopes{\text{ }}of{\text{ }}{l_4}) = - 1 \\\ slopes{\text{ }}of{\text{ }}{l_4} = \dfrac{{ - 4}}{3} \\\$$

Equation of a line joining point $({x_1},{y_1})$ and having the slope ‘m’
$(y - {y_1}) = m(x - {x_1})$
Equation of ${l_4},$
$(y - 0) = \dfrac{{ - 4}}{3}(x + 2) \\\ \Rightarrow 3y = - 4x - 8 \\\ \Rightarrow 4x + 3y + 8 = 0 \\\$
Hence, Option (A) is the correct option.
Note: We can find the slope of ${l_3}$without finding the line equation of ${l_3}$as
The slope of a line passing through two points $({x_1},{y_1})$ and $({x_2},{y_2})$is given by
$slope = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}$

$$The{\text{ }}slope{\text{ }}of{\text{ }}the{\text{ }}line({l_3}) = \dfrac{{3 - 0}}{{2 - ( - 2)}} \\\ = \dfrac{3}{4} \\\$$