Question

Given that, u is a vector of length 2, v is a vector of length 3, and the angle between them, when placed tail to tail is ${{45}^{\circ}}$, which option is closest to the exact value of $\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,$?
a) 4.5
b) 6.2
c) 4.2
d) 5.1

Answer 1

As we are having two vectors $\overset{\to }{\mathop{u}}\,$ and $\overset{\to }{\mathop{v}}\,$whose magnitude is given as: $\left| \overset{\to }{\mathop{u}}\, \right|=2$and $\left| \overset{\to }{\mathop{v}}\, \right|=3$, and the angle between them is ${{45}^{\circ }}$. We need to find the value of $\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,$. By using the dot product formula: $\overset{\to }{\mathop{a}}\,.\overset{\to }{\mathop{b}}\,=\left| \overset{\to }{\mathop{a}}\, \right|\left| \overset{\to }{\mathop{b}}\, \right|\cos \theta$, where $\theta$ is the angle between the vectors find the value of $\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,$

Complete step-by-step solution:
We are given that $\left| \overset{\to }{\mathop{u}}\, \right|=2$and $\left| \overset{\to }{\mathop{v}}\, \right|=3$, and the angle between them is ${{45}^{\circ }}$ as shown in the diagram below:

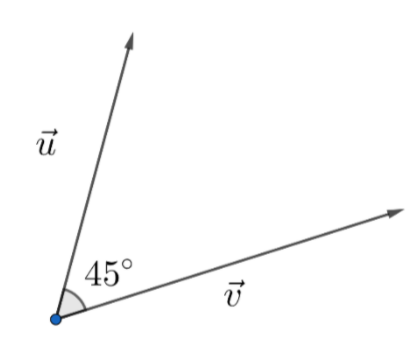
Now, by applying dot product formula for vectors $\overset{\to }{\mathop{u}}\,$ and $\overset{\to }{\mathop{v}}\,$, we get:
$\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,=\left| \overset{\to }{\mathop{u}}\, \right|\left| \overset{\to }{\mathop{v}}\, \right|\cos \theta ......(1)$
Since we know that: $\left| \overset{\to }{\mathop{u}}\, \right|=2$and $\left| \overset{\to }{\mathop{v}}\, \right|=3$ and $\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$
Now, substitute the values in equation (1), we get:
$\begin{aligned} & \overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,=2\times 3\times \dfrac{1}{\sqrt{2}} \\\ & =\dfrac{6}{\sqrt{2}}......(2) \end{aligned}$
Now, we can rationalize equation (2) by multiplying and dividing the equation by $\sqrt{2}$.
We get:
$\begin{aligned} & \overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,=\dfrac{6}{\sqrt{2}}\times \dfrac{\sqrt{2}}{\sqrt{2}} \\\ & =\dfrac{6\sqrt{2}}{2} \\\ & =3\sqrt{2}......(3) \end{aligned}$
Since, $\sqrt{2}=1.41$, so the value of dot product of $\overset{\to }{\mathop{u}}\,$ and $\overset{\to }{\mathop{v}}\,$ is:
$\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,=4.23$ which is closest to 4.5
Hence, option (a) is the correct answer.

Note: As it is mentioned that the length of $\overset{\to }{\mathop{u}}\,$ is 2, and length of $\overset{\to }{\mathop{v}}\,$ is 3, students might misplace the values because it is the magnitude of the vectors given, not the vector itself.
So, they might directly multiply 2 and 3 and get 6 as an answer, which is the wrong choice. Students need to read the question carefully and then substitute the values accordingly, whether the magnitude is given or the vector is given.