Solveeit Logo
Login

Question

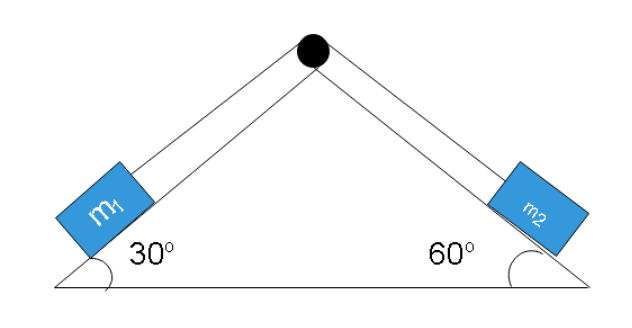
Question: Given that \({m_1} = \,10\,kg\) and \({m_2} = 12\,kg\) connected as shown in the figure given below....

Given that m1= 10 kg{m_1} = \,10\,kg and m2=12 kg{m_2} = 12\,kg connected as shown in the figure given below. Find tension in the string and acceleration of the two blocks.

Explanation

Solution

In this solution, we will find the components of the blocks that will exert tension on the string i.e. parallel to the slope of the inclined plane. Both the blocks will have the same acceleration since they are connected with a string which will be under constant tension.

Complete step by step answer:
Looking at the figure, the block of mass 12 kg will be heavier and as a result, it will move downwards and at the same time, pull the block of mass 10 kg upwards. Both the block will have the same acceleration since they are tied by the same string under acceleration and hence the same tension in the string as well.
Since the block of mass 10 kg will be moving upwards, the pseudo acceleration force and the tension in the string will both be towards the pulley, parallel to the surface of the power and the component of the weight for the block will be downwards. So, we can write
m1a=T−m1gsin⁡θ1{m_1}a = T - {m_1}g\sin {\theta _1}
⇒T=m1gsin⁡θ1+m1a\Rightarrow T = {m_1}g\sin {\theta _1} + {m_1}a
Similarly, for the second block, we can write, the weight and the acceleration will be downwards
m2a=m2gsin⁡θ2−T{m_2}a = {m_2}g\sin {\theta _2} - T
⇒T=m2gsin⁡θ2−m2a\Rightarrow T = {m_2}g\sin {\theta _2} - {m_2}a
So comparing tension in both these equations, we can write
12m1g+m1a=32m2g−m2a\dfrac{1}{2}{m_1}g + {m_1}a = \dfrac{{\sqrt 3 }}{2}{m_2}g - {m_2}a
Solving for aa, we get
22a=32(12)g−12(10)g22a = \dfrac{{\sqrt 3 }}{2}(12)g - \dfrac{1}{2}(10)g
On substituting g=10 m/s2g = 10\,m/{s^2}, we get
22a=5422a = 54
Hence a=2.45 m/s2a = 2.45\,m/{s^2}
Then the tension in the string can be calculated as
T=m1gsin⁡θ1+m1aT = {m_1}g\sin {\theta _1} + {m_1}a
⇒T=50+24.5\Rightarrow T = 50 + 24.5
Hence the tension in the string will be
T=74.5 NT = 74.5\,N

Note: Here we have assumed that there is no friction acting on the blocks and the ramps which can hinder the motion of the blocks. Since the second block is heavier and also at a more inclined plane, we can assume that it will be pulling the first block.