Question

Given that, for all the real values of x, the expression $\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}$ lies between $\dfrac{1}{3}\text{and }3$. The values between which the expression $\dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}$ lies are
a. 0 and 2
b. -1 and 1
c. -1 and 0
d. $\dfrac{1}{3}\text{and }3$

Answer 1

We will first assume $y=\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}$ and on further solving this, we get an equation, ${{x}^{2}}\left( 1-y \right)-2x\left( 1+y \right)+4-4y=0$ which is a quadratic equation and we know that discriminant of quadratic equation ${{b}^{2}}-4ac$ must be greater than 0 for any real value of roots. On solving the discriminant, we get to know that the range of $y\in \left[ \dfrac{1}{3},3 \right]$ as its independent of x. Then, in the final step, we will write, $\dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}$ as $\dfrac{{{\left( {{3.3}^{x}} \right)}^{2}}-2{{\left( 3.3 \right)}^{x}}+4}{{{\left( {{3.3}^{x}} \right)}^{2}}+2{{\left( 3.3 \right)}^{x}}+4}$ and find the range of the expression.

Complete step-by-step solution:
It is given in the question that for all the real values of x, the expression $\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}$ lies between $\dfrac{1}{3}\text{and }3$. Then we have to find the values between which the expression $\dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}$ lies.
Let us first assume the expression $y=\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}$. On cross multiplying both the sides, we get,
$\begin{aligned} & y\left( {{x}^{2}}+2x+4 \right)={{x}^{2}}-2x+4 \\\ & {{x}^{2}}y+2xy+4y={{x}^{2}}-2x+4 \\\ \end{aligned}$
On transposing all the terms on the LHS to the RHS, we get,
$\begin{aligned} & {{x}^{2}}-2x+4-{{x}^{2}}y-2xy-4y \\\ & {{x}^{2}}-{{x}^{2}}y-2x-2xy+4-4y \\\ & {{x}^{2}}\left( 1-y \right)-2x\left( 1+y \right)+4\left( 1-y \right)=0 \\\ \end{aligned}$
Now, it is a quadratic equation and we know that in a quadratic equation, the discriminant ${{b}^{2}}-4ac$ must be greater than 0 for any real value of roots.
So, from the quadratic equation, we have a = (1 - y), b = -2 (1 + y) and c = 4 (1 – y).
So, we have the discriminant, $d={{b}^{2}}-4ac$ and we know that d must be greater than 0, so we can write,
$\begin{aligned} & d={{b}^{2}}-4ac\ge 0 \\\ & ={{\left[ -2\left( 1+y \right) \right]}^{2}}-4\left[ \left( 1-y \right)\left( 4 \right)\left( 1-y \right) \right]\ge 0 \\\ & =4{{\left( 1+y \right)}^{2}}-16{{\left( 1-y \right)}^{2}}\ge 0 \\\ \end{aligned}$
On taking 4 common from both the terms, we get,
$\begin{aligned} & =4\left[ {{\left( 1+y \right)}^{2}}-4{{\left( 1-y \right)}^{2}} \right]\ge 0 \\\ & =\left[ {{\left( 1+y \right)}^{2}}-4{{\left( 1-y \right)}^{2}} \right]\ge 0 \\\ \end{aligned}$
We know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ and ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we get,
$\begin{aligned} & ={{1}^{2}}+{{y}^{2}}+2\left( 1 \right)\left( y \right)-4\left[ {{1}^{2}}+{{y}^{2}}-2\left( 1 \right)\left( y \right) \right]\ge 0 \\\ & =1+{{y}^{2}}+2y-4\left[ 1+{{y}^{2}}-2y \right]\ge 0 \\\ \end{aligned}$
On opening the bracket, we get,
$=1+{{y}^{2}}+2y-4-4{{y}^{2}}+8y\ge 0$
On further simplifying, we get,
$=-3{{y}^{2}}+10y-3\ge 0$
On multiplying both the sides by (-1), we get,
$=3{{y}^{2}}-10y+3\le 0$
Here, the sign of the inequality changes as we have multiplied the expression with a negative number. Now, we can split -10y as -9y –y, so we get,
$\begin{aligned} & =3{{y}^{2}}-9y-y+3\le 0 \\\ & =3y\left( y-3 \right)-\left( y-3 \right)\le 0 \\\ & =\left( 3y-1 \right)\left( y-3 \right)\le 0 \\\ & \left( 3y-1 \right)=0\text{ }or\left( y-3 \right)=0 \\\ & y=\dfrac{1}{3}or3 \\\ \end{aligned}$
Now, we will plot $\dfrac{1}{3}\text{and }3$ on the number line.

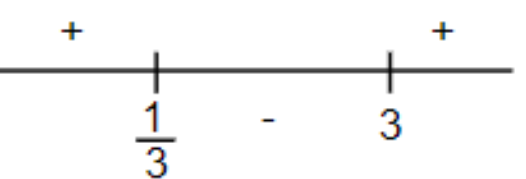
If we put 0 in $\left( 3y-1 \right)\left( y-3 \right)\le 0$, we get, (-1) (-3) = 3, and it is a positive term.
Again, if we put 1 in $\left( 3y-1 \right)\left( y-3 \right)\le 0$, we get, (2) (-2) = -4, and it is a negative term.
And we put 4 in $\left( 3y-1 \right)\left( y-3 \right)\le 0$, we get, (11) (1) = 11, and it is a positive term.
Hence, we can show the number line as,
Thus, we get a region $\left[ \dfrac{1}{3},3 \right]$ where the range is $y\in \left[ \dfrac{1}{3},3 \right]$.
Also, $\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}\in \left[ \dfrac{1}{3},3 \right]$
This means that the range does not depend on x, but it depend on y.
Now, we have been given the expression, $\dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}$. So, we can write,
$\begin{aligned} & \dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}=\dfrac{{{3}^{2}}{{.3}^{2x}}-2\left( {{3.3}^{x}} \right)+4}{{{3}^{2}}{{.3}^{2x}}+2\left( {{3.3}^{x}} \right)+4} \\\ & =\dfrac{{{\left( {{3.3}^{x}} \right)}^{2}}-2{{\left( 3.3 \right)}^{x}}+4}{{{\left( {{3.3}^{x}} \right)}^{2}}+2{{\left( 3.3 \right)}^{x}}+4} \\\ \end{aligned}$
Let us assume that $\left( {{3.3}^{x}} \right)$ equal to u, so we get,
$\dfrac{{{\left( u \right)}^{2}}-2u+4}{{{\left( u \right)}^{2}}+2u+4}$
Now, if we compare $\dfrac{{{\left( u \right)}^{2}}-2u+4}{{{\left( u \right)}^{2}}+2u+4}$ and $\dfrac{{{x}^{2}}-2x+4}{{{x}^{2}}+2x+4}$, we get to know that both are similar. We also know that the range of the expression will depend upon y and not x, so it will also not depend on u.
Thus, the range of the expression, $\dfrac{{{9.3}^{2x}}-{{6.3}^{x}}+4}{{{9.3}^{2x}}+{{6.3}^{x}}+4}$ will lie between $\left[ \dfrac{1}{3},3 \right]$.
Hence, option (d) is the correct answer.

Note: Most of the students make mistake after multiplying the expression, $-3{{y}^{2}}+10y-3\ge 0$ with (-1). They may directly write it as $3{{y}^{2}}-10y+3\ge 0$, but this is wrong and will lead to wrong answers. After multiplying the expression with (-1), the sign of the inequality should change and the expression should be $3{{y}^{2}}-10y+3\le 0$. This question has high chances of calculation errors, so the students are advised to solve this question step by step and carefully.