Question

Given that for a, b, c, d ∈ R, if a sec (200°) - c tan (200°) = d and b sec (200°) + d tan(200°) = c then $\frac{a^2 + b^2 + c^2 + d^2}{ac - bd}$ = pcosec (200°) find the value of p .

Answer 1

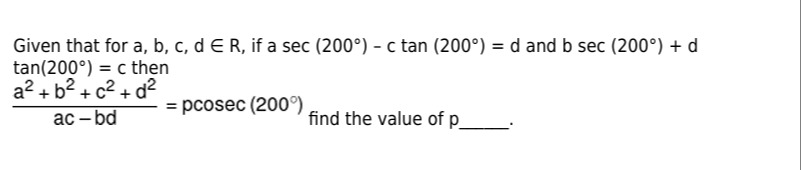
2

Answer 2

Let the given equations be:

1. $a \sec(200^\circ) - c \tan(200^\circ) = d$
2. $b \sec(200^\circ) + d \tan(200^\circ) = c$

Let $x = 200^\circ$. The equations become:

1. $a \sec x - c \tan x = d$
2. $b \sec x + d \tan x = c$

Multiply both equations by $\cos x$ (note that $\cos(200^\circ) \neq 0$):

1. $a - c \sin x = d \cos x \implies a = d \cos x + c \sin x$
2. $b + d \sin x = c \cos x \implies b = c \cos x - d \sin x$

We need to evaluate the expression $\frac{a^2 + b^2 + c^2 + d^2}{ac - bd}$.

First, let's calculate $a^2 + b^2$: $a^2 = (d \cos x + c \sin x)^2 = d^2 \cos^2 x + c^2 \sin^2 x + 2cd \cos x \sin x$ $b^2 = (c \cos x - d \sin x)^2 = c^2 \cos^2 x + d^2 \sin^2 x - 2cd \cos x \sin x$ Adding $a^2$ and $b^2$: $a^2 + b^2 = (d^2 \cos^2 x + c^2 \sin^2 x + 2cd \cos x \sin x) + (c^2 \cos^2 x + d^2 \sin^2 x - 2cd \cos x \sin x)$ $a^2 + b^2 = d^2 (\cos^2 x + \sin^2 x) + c^2 (\sin^2 x + \cos^2 x)$ Using the identity $\sin^2 x + \cos^2 x = 1$: $a^2 + b^2 = d^2(1) + c^2(1) = c^2 + d^2$.

Now, the numerator of the expression is $a^2 + b^2 + c^2 + d^2$. $a^2 + b^2 + c^2 + d^2 = (c^2 + d^2) + c^2 + d^2 = 2(c^2 + d^2)$.

Next, let's calculate the denominator $ac - bd$: $ac = (d \cos x + c \sin x) c = cd \cos x + c^2 \sin x$ $bd = (c \cos x - d \sin x) d = cd \cos x - d^2 \sin x$ Subtracting $bd$ from $ac$: $ac - bd = (cd \cos x + c^2 \sin x) - (cd \cos x - d^2 \sin x)$ $ac - bd = cd \cos x + c^2 \sin x - cd \cos x + d^2 \sin x$ $ac - bd = c^2 \sin x + d^2 \sin x = (c^2 + d^2) \sin x$.

Now substitute the expressions for the numerator and the denominator into the given fraction: $\frac{a^2 + b^2 + c^2 + d^2}{ac - bd} = \frac{2(c^2 + d^2)}{(c^2 + d^2) \sin x}$.

For this expression to be defined, we must have $ac - bd \neq 0$, which means $(c^2 + d^2) \sin x \neq 0$. Since $x = 200^\circ$, $\sin(200^\circ) = \sin(180^\circ + 20^\circ) = -\sin(20^\circ) \neq 0$. Thus, we must have $c^2 + d^2 \neq 0$. If $c^2 + d^2 \neq 0$, we can cancel the term $(c^2 + d^2)$: $\frac{2(c^2 + d^2)}{(c^2 + d^2) \sin x} = \frac{2}{\sin x}$.

We are given that $\frac{a^2 + b^2 + c^2 + d^2}{ac - bd} = p \operatorname{cosec}(200^\circ)$. Substituting the evaluated expression: $\frac{2}{\sin(200^\circ)} = p \operatorname{cosec}(200^\circ)$. Since $\operatorname{cosec}(200^\circ) = \frac{1}{\sin(200^\circ)}$, we have: $\frac{2}{\sin(200^\circ)} = p \frac{1}{\sin(200^\circ)}$.

Since $\sin(200^\circ) \neq 0$, we can multiply both sides by $\sin(200^\circ)$: $2 = p$.

The value of $p$ is 2.

Note: If $c^2 + d^2 = 0$, then $c=0$ and $d=0$ (since $c, d \in \mathbb{R}$). The original equations become:

1. $a \sec(200^\circ) = 0 \implies a = 0$ (since $\sec(200^\circ) \neq 0$)
2. $b \sec(200^\circ) = 0 \implies b = 0$ (since $\sec(200^\circ) \neq 0$) In this case, $a=b=c=d=0$. The expression $\frac{a^2 + b^2 + c^2 + d^2}{ac - bd}$ becomes $\frac{0}{0}$, which is indeterminate. However, the problem states that this expression equals $p \operatorname{cosec}(200^\circ)$. Since $\operatorname{cosec}(200^\circ) \neq 0$, the right side is non-zero if $p \neq 0$. An indeterminate form cannot equal a specific non-zero value. This confirms that the case $c^2 + d^2 = 0$ is not the scenario described by the problem.

The final answer is $\boxed{2}$.