Question

Given that: ${a_n} = \arctan (2n)$ is the sequence seems to be infinite solution. Tell whether it converges or diverges?
(a) Converges
(b) Diverges
(c) Cannot be Determined
(d) None of the above

Answer 1

Hint : In the given question, we are going to use the expression for basic continuity formula which tends to infinity ‘ $\infty$ ’ for the respective sequence of limit say, $\mathop {\lim }\limits_{x \to \infty } f[g(x)] = f\left[ {\mathop {\lim }\limits_{x \to \infty } g(x)} \right]$ assumed and then substituting it in to the formula (showing on graphically with curve from left to right tends to positive infinity). Then, we will simplify it by substituting the given sequence to get the required answer.

Complete step-by-step answer :
First, let us consider that the function $f(x) = {a_n}$ and $g(x) = \arctan (2n)$ exists.
$\mathop {\lim }\limits_{n \to \infty } {a_n} = \mathop {\lim }\limits_{n \to \infty } \arctan (2n)$
Where, the sequence tends to infinity ‘ $\infty$ ’ ….. ( $\because$ Given)
Let’s assume that, the given function implies the condition below which seems to be convergent only if in the following circumstance exists,
$\mathop {\lim }\limits_{x \to \infty } f[g(x)] = f\left[ {\mathop {\lim }\limits_{x \to \infty } g(x)} \right]$
Here, the variable is ‘n‘ which may vary as per the requirement.
As a result, substituting the given functions in the above formula, we get
$\mathop { \Rightarrow \lim }\limits_{n \to \infty } {a_n} = \arctan \left( {\mathop {\lim }\limits_{n \to \infty } 2n} \right)$
Also, since by drawing the graphical representation it can be clearly assumed that,

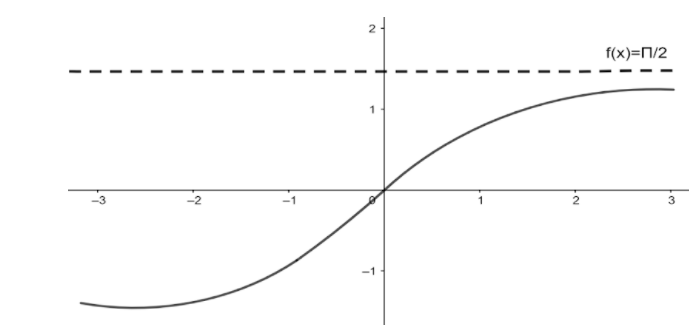
$\Rightarrow$ The variable ‘ $x$ ’ tends to $\dfrac{\pi }{2}$ as the curve or arc passes from left to right up to infinity.
$\therefore \Rightarrow \mathop {\lim }\limits_{n \to \infty } {a_n} = \arctan \left( \infty \right)$
Since, anything multiplied by infinity is equal to $\dfrac{\pi }{2}$
$\Rightarrow \mathop {\lim }\limits_{n \to \infty } {a_n} = \dfrac{\pi }{2}$
Therefore, the sequence satisfies the given function which converges at $\dfrac{\pi }{2}$ respectively
$\Rightarrow \therefore$ The option (a) is correct!
So, the correct answer is “Option a”.

Note : One must know the limits (continuity) concept along with graphical representation to solve the question. Continuity equation $\mathop {\lim }\limits_{x \to \infty } f[g(x)] = f\left[ {\mathop {\lim }\limits_{x \to \infty } g(x)} \right]$ can be stated that the value satisfies the equation upto the tended value say, $\infty$ . As a result, by putting the given values in the function the required answer can be obtained. One must take care of the calculations to be sure of the final answer by multiplying with infinity.