Question

Given,$^{{\text{227}}}{\text{Ac}}$ has a half-life of $22$ years with respect to radioactive decay. The decay follows two parallel paths: $^{{\text{227}}}{\text{Ac}}{ \to ^{{\text{227}}}}{\text{Th}}$ and $^{{\text{227}}}{\text{Ac}}{ \to ^{{\text{227}}}}{\text{Fr}}$. If the percentage of the two daughter nuclides at ${\text{2}}{\text{.0}}$ and ${\text{98}}{\text{.0}}$ respectively, the decay constant (in year-1) for $^{{\text{227}}}{\text{Ac}}{ \to ^{{\text{227}}}}{\text{Th}}$ path is closest to
A) $6.3 \times {10^{ - 2}}$
B) $6.3 \times {10^{ - 3}}$
C) $6.3 \times {10^{ - 1}}$
D) $6.3 \times {10^{ - 4}}$

Answer 1

Radioactive decay has two important terms related to it, Half-life and Decay constant. we'll define both the terms and can find a relation between the 2 . The relations are often obtained by using the expression of decay law.

Complete step by step answer:
Radioactive decay is described because the process by which an unstable atomic nucleus loses energy by radiation. A sample material containing radioactive nuclei is taken into account radioactive. The decay of radioactive elements occurs at a hard and fast constant rate. The half-life of a radioisotope is the time required for one half the concentration of the unstable substances to degrade into a more stable material. We will say that half-life is the time required for a radioactive sample to scale back to half its initial value. The half-life of a radioactive sample is represented by ${T_{1/2}}$.Decay constant is that the proportionality between the dimensions of a population of radioactive atoms and therefore the rate at which the population decreases due to decay. The decay constant is represented by the symbol ${\lambda }$.

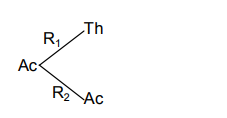
Now we calculate the % of ${\text{Th}}$
$\% {\text{Th = }}\dfrac{{{{\text{R}}_{\text{1}}}}}{{{{\text{R}}_{\text{T}}}}}{\text{ = }}\dfrac{{\text{2}}}{{{\text{100}}}}$
Similarly we calculate the % of ${\text{Ac}}$
$\% {\text{Ac = }}\dfrac{{{{\text{R}}_2}}}{{{{\text{R}}_{\text{T}}}}}{\text{ = }}\dfrac{{98}}{{{\text{100}}}}$
$\therefore \dfrac{{{{\text{R}}_{\text{1}}}}}{{{{\text{R}}_{\text{2}}}}} = \dfrac{2}{{98}}$
Hence ${{\text{R}}_{\text{T}}}{\text{ = }}{{\text{R}}_{\text{1}}}{\text{ + }}{{\text{R}}_{\text{2}}}$
$\dfrac{{0.693}}{{22}} = {{\text{R}}_{\text{1}}}{\text{ + }}\dfrac{{{\text{98}}}}{{\text{2}}}{{\text{R}}_{\text{1}}}$
$\therefore {{\text{R}}_1} = 6.3 \times {10^{ - 4}}$
Hence the correct option is answer D.

Note:
Half-life means how much time a radioactive sample takes to become half of its original concentration, while decay constant is a probability of decay per unit time. Half-life of a radioactive sample depends on the elimination rate of sample and the initial concentration of the sample, while decay constant is fixed for a particular radioactive nuclide.