Question
Question: given: $\sum_{R=1}^{\infty} \frac{1}{R^2} = \frac{\pi^2}{6}.$ $S_i = \sum_{k=1}^{\infty} \frac{1}{(...
given: ∑R=1∞R21=6π2.
Si=∑k=1∞(36k2−1)1∗i
find S1+S2
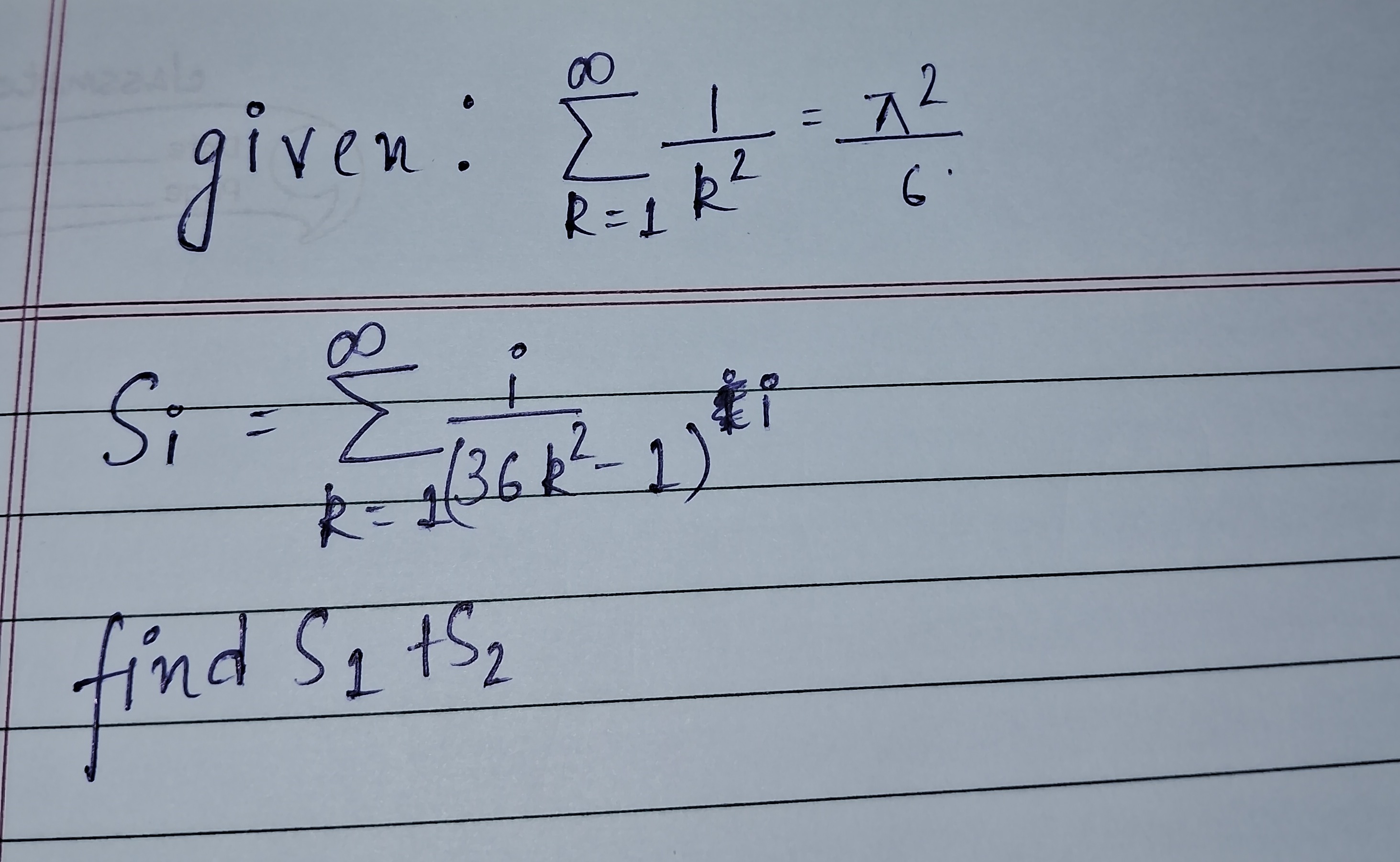
23−4π3
Solution
Let S=∑k=1∞36k2−11. The expression Si is given by Si=i⋅S. We need to find S1+S2=1⋅S+2⋅S=3S.
To evaluate S, we use the partial fraction decomposition of the term 36k2−11. Using the difference of squares formula, 36k2−1=(6k)2−12=(6k−1)(6k+1). We can write: 36k2−11=(6k−1)(6k+1)1 Using partial fractions: (6k−1)(6k+1)1=6k−1A+6k+1B Multiplying by (6k−1)(6k+1): 1=A(6k+1)+B(6k−1) Setting 6k−1=0⟹k=1/6: 1=A(1+1)⟹2A=1⟹A=1/2. Setting 6k+1=0⟹k=−1/6: 1=B(−1−1)⟹−2B=1⟹B=−1/2. So, 36k2−11=21(6k−11−6k+11) Now, we can evaluate the sum S: S=∑k=1∞21(6k−11−6k+11)=21∑k=1∞(6k−11−6k+11) This sum can be evaluated using the Mittag-Leffler expansion for the cotangent function, or by relating it to a known series summation formula. A standard result for sums of the form ∑n=1∞n2−a21 is: ∑n=1∞n2−a21=2a21−2aπcot(πa) We can rewrite our sum S by considering a related sum: ∑n=1∞36n2−11=∑n=1∞(6n)2−121 Let a=1/6. Then a2=1/36. ∑n=1∞n2−(1/6)21=∑n=1∞36n2−136=36S Using the formula: 36S=2(1/6)21−2(1/6)πcot(π/6) 36S=2(1/36)1−1/3πcot(π/6) 36S=18−3πcot(π/6) Since cot(π/6)=3: 36S=18−3π3 Dividing by 36: S=3618−3π3=21−12π3 We need to find S1+S2. S1=1⋅S=21−12π3. S2=2⋅S=2(21−12π3)=1−6π3. S1+S2=(21−12π3)+(1−6π3) S1+S2=21+1−12π3−122π3 S1+S2=23−123π3 S1+S2=23−4π3 The given information ∑R=1∞R21=6π2 is not directly used in this solution method but is a well-known result related to infinite series.
