Question

Given,${S_1},{S_2}$ are foci of an ellipse of major axis of length 10 units and P is any point on the ellipse such that perimeter of triangle $P{S_1}{S_2}$is 15. Then eccentricity of the ellipse is:
A.0.5
B.0.25
C.0.28
D.0.75

Answer 1

We know that the sum of whose distances from two fixed points in the plane is a constant. These two fixed points are called the foci of the ellipse, foci is the plural of focus of the ellipse. The line segment joining the foci is called as the major axis, and the line perpendicular to it passing through the center of the ellipse is called as the minor axis of the ellipse.

Complete answer:
Here given that the length of the major axis is 10 units, which is generally denoted by 2a.
$\Rightarrow 2a = 10$
$\Rightarrow a = 5$
The points ${S_1}$ and ${S_2}$ are the foci of the ellipse. The point P is on the ellipse.
Given that the perimeter of the triangle of vertices $P,{S_1},{S_2}$ is 15.

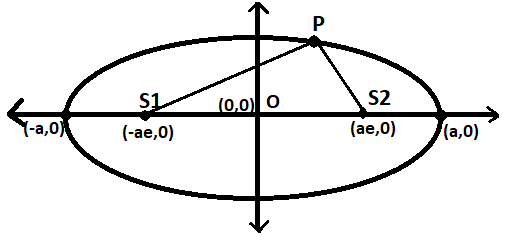
The perimeter of the triangle $P{S_1}{S_2}$ is given by:
$\Rightarrow P{S_1} + P{S_2} + {S_1}{S_2} = 15$
Finding ${S_1}{S_2}$, the distance between ${S_1}$and ${S_2}$is given by:
$\Rightarrow {S_1}{S_2} = \sqrt {{{( - ae - ae)}^2} + {{(0 - 0)}^2}}$
$\Rightarrow {S_1}{S_2} = \sqrt {{{(2ae)}^2}}$
$\Rightarrow {S_1}{S_2} = 2ae$
Now finding the value of $P{S_1} + P{S_2}$, which is constant as already discussed before in the definition of the ellipse i.e, the sum of whose distances from two fixed points in the plane is a constant. Here the two fixed points are points ${S_1}$ and ${S_2}$, which are the foci are the ellipse. P is any point on the ellipse, then :
$\Rightarrow P{S_1} + P{S_2} =$ constant
P can be anywhere on the ellipse but the above expression holds true.
So let the point P be one of the vertices of the ellipse, which is on the ellipse, which is (a,0).
$\therefore$Let $P = (a,0)$

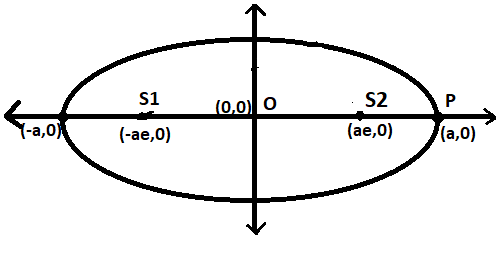
Now calculating the $P{S_1} + P{S_2}$:
First calculating $P{S_1}$:
$\Rightarrow P{S_1} = P{S_2} + {S_2}O + O{S_1}$
Here the length of$P{S_2} = a(1 - e)$
The length of ${S_2}O = ae$
The length of $O{S_1} = ae$
$\therefore P{S_1} = a(1 - e) + ae + ae$
$\Rightarrow P{S_1} = a + ae$
Now we already know that $P{S_2} = a(1 - e)$.
$\therefore P{S_1} + P{S_2} = a + ae + a(1 - e)$
$\Rightarrow P{S_1} + P{S_2} = a + ae + a - ae$
$\therefore P{S_1} + P{S_2} = 2a$
And ${S_1}{S_2} = 2ae$
The perimeter of the triangle $P{S_1}{S_2}$ is 15 :
$\Rightarrow P{S_1} + P{S_2} + {S_1}{S_2} = 15$
$\Rightarrow 2a + 2ae = 15$
$\Rightarrow 2a(1 + e) = 15$
We know that a=5, substituting in the above expression to get the value of e, eccentricity if the ellipse:
$\Rightarrow 2(5)(1 + e) = 15$
$\Rightarrow 10(1 + e) = 15$
$\Rightarrow (1 + e) = \dfrac{{15}}{{10}}$
$\Rightarrow (1 + e) = 1.5$
$\Rightarrow e = 1.5 - 1$
$\Rightarrow e = 0.5$
Final Answer: The eccentricity of the ellipse is 0.5

So Option A is the correct answer.

Note:
It is very important to remember that the most important fact of the ellipse which is, the sum of whose distances from two fixed points in the plane is a constant. The constant is always equal to 2a, where 2a is the length of the major axis of the ellipse.