Question
Question: Given: \(\overline{AB}\) and \(\overline{CD}\) intersect at \(O\) and the endpoints of \(\overline{A...
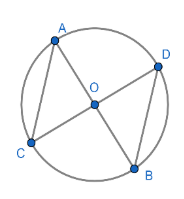
Given: AB and CD intersect at O and the endpoints of AB and CD are on circle O.
Prove: AC≅BD
Solution
Hint: We can apply the cosine rule to find the angles ∠AOC and ∠BOD and hence establish a relation between the sides AC and BD.
Complete Step-by-Step Solution:
It is given in the question that ABand CD intersect at O. It is also given that the endpoints of AB and CD are on circle O.
So, we can draw a figure from the data given in the question as shown below.
Let us consider that the circle has a radius r and has its centre at point O. Since O is the centre of the circle and the points A,B,C,D lie on the circumference of the circle, we can obtain the following relation:
OA=OB=OC=OD=r
Let us assume that the angle ∠AOC=θ.
Since ∠AOC and ∠BOD are vertically opposite angles, they will be the same. Therefore, we can write that
∠AOC=θ
∠BOD=θ
Now, let us consider a triangle with sides a,b,c and angle αas shown in the figure below,
cosα=2aba2+b2−c2................(i)
The above formula is called the cosine rule. Generally, we know that the cosine of any angle in a right-angled triangle is equal to the ratio of the base to the hypotenuse. But the cosine rule can be applied to any triangle, be it an acute triangle, obtuse triangle or a right-angled triangle.
Using the cosine rule (i) in ∠AOC, we get
cosθ=2r2r2+r2−(AC)2
⇒2r2cosθ=2r2−(AC)2
⇒(AC)2=2r2−2r2cosθ............(ii)
Using the cosine rule (i) in ∠BOD, we get
cosθ=2r2r2+r2−(BD)2
⇒2r2cosθ=2r2−(BD)2
⇒(BD)2=2r2−2r2cosθ................(iii)
If we compare the equations (ii) and (iii), we get that
(AC)2=(BD)2
⇒(AC)=(BD)
Therefore, it states that the length ofAC is equal to the length of BD.
AC≅BD
Hence proved.
Note: This question uses the concepts of circles and also requires the knowledge of cosine rule, which is a concept of the properties of a triangle. In order to find the relation between AC and BD, one has to use the cosine rule.
