Question
Question: Given\[n(A) = 285,n(B) = 195,n(U) = 500,n(A \cup B) = 410\], find \[n(A' \cup B')\]...
Givenn(A)=285,n(B)=195,n(U)=500,n(A∪B)=410, find n(A′∪B′)
Solution
Venn diagrams are used to represent the relation between the sets. Here, the number of sets A, B, and their union have been given and we need to find the union of its complementary sets. We will use the suitable formula of sets to find the unknown terms.
Formula: Some of the formulas we need to know:
1.n(A∪B)=n(A)+n(B)−n(A∩B)
2.n(A′∪B′)=n(A∩B)′=n(U)−n(A∩B)
Complete step by step answer:
It is given that n(A)=285,n(B)=195,n(U)=500,n(A∪B)=410
We aim to find the value of the term n(A′∪B′). We can use the formula n(A′∪B′)=n(A∩B)′=n(U)−n(A∩B) to find the value n(A′∪B′). We have the value n(U)but we don’t know the value of n(A∩B) we need to find that.
Let us consider the formula n(A∪B)=n(A)+n(B)−n(A∩B).
Let us draw the Venn diagram for a clear representation.
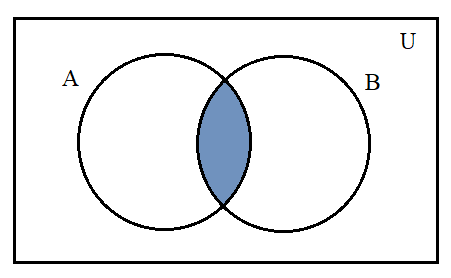
n(A∪B)
n(A)
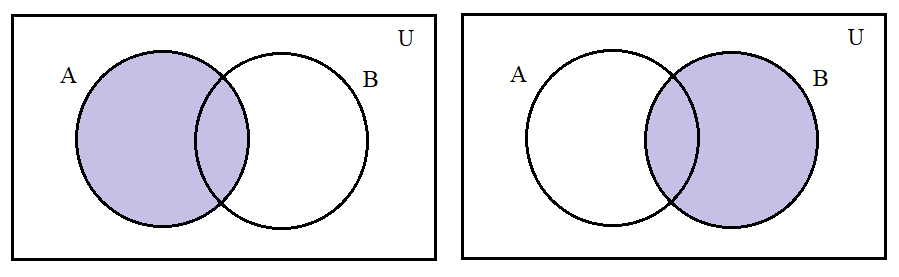
n(B)
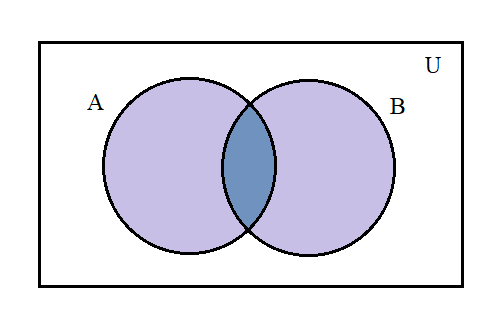
n(A∩B)
If we see that there was an overlap at the intersection part when we add n(A)& n(B)so, we will get two parts of n(A∩B). When we subtract one part of the term n(A∩B)we will getn(A∪B).
In this, we have the value of n(A),n(B)&n(A∪B) using this we can find the value of n(A∩B).
Let us substitute the values we have in the formula n(A∪B)=n(A)+n(B)−n(A∩B).
n(A \cup B) = n(A) + n(B) - n(A \cap B)$$$$ \Rightarrow 410 = 285 + 195 - n(A \cap B)
Let us simplify this to find the value ofn(A∩B). Let us taken(A∩B) to the other side and shift 410 to the right side.
⇒n(A∩B)=285+195−410
On simplifying this we get
⇒n(A∩B)=480−410
⇒n(A∩B)=70
Thus, we got the value ofn(A∩B)=70.
Now we can find the value ofn(A′∪B′). Let us now use the formula n(A′∪B′)=n(A∩B)′=n(U)−n(A∩B)and substitute the values ofn(U)&n(A∩B).
Let us first draw a Venn diagram.
We know thatn(A′∪B′)=n(A∩B)′. Let’s draw the Venn diagram for this.
n(A′∪B′)=n(A∩B)′

n(U)
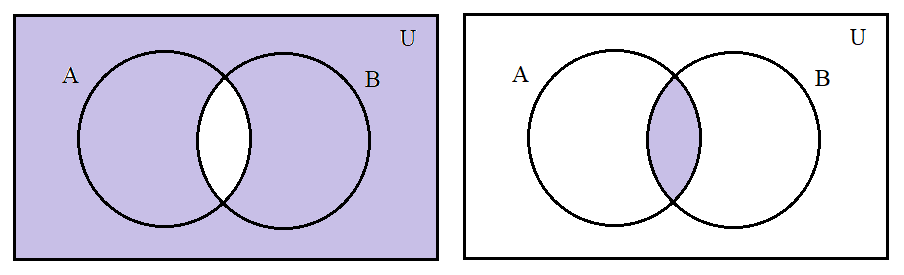
n(A∩B)
Thus, when we subtract n(A∩B) from n(U) we get n(A′∪B′)orn(A∩B)′.
On substituting the values ofn(U)=500&n(A∩B)=70 inn(A′∪B′)=n(A∩B)′=n(U)−n(A∩B) we get
n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)$$$$ \Rightarrow 500 - 70
On simplifying this we get
⇒n(A′∩B′)=430
Thus, we have found the value of the termn(A∩B)=430.
Note: It is important to choose the correct formula because there may be some formula giving the value that we need but they won’t contain the terms we have so we need to find the values that we don’t have and use that to find the value that we want.
