Question
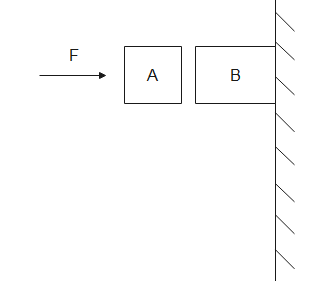
Question: Given in the figure are two blocks A and B of weight \(30N\) and \(100N\). These are being pressed a...
Given in the figure are two blocks A and B of weight 30N and 100N. These are being pressed against a wall by a force Fas shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on the block is
(A). 100N
(B). 70N
(C). 120N
(D). 150N
Solution
An external force is pressing the blocks to the wall; there exists frictional force between the blocks and between block and wall. Taking each block as a separate system and resolving the forces acting on each block we get some equations, we can solve the equations to calculate frictional force between block and wall.
Formulas used:
f=30N
f−f′=100N
Complete answer:
The frictional force is a force that opposes the motion of an object. It acts opposite to the motion of an object. Here the frictional force prevents the sliding of block B against the wall and the sliding of blocks against each other
The frictional force is given by-
Fμ=μN - (1)
Here, Fμ is the frictional force
μ is the coefficient of friction
N is the normal reaction between the surfaces
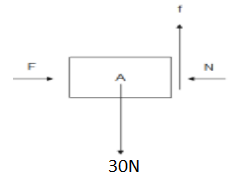
From the above figure, we can say that
f=30N
Here, f is the frictional force acting between both the blocks.
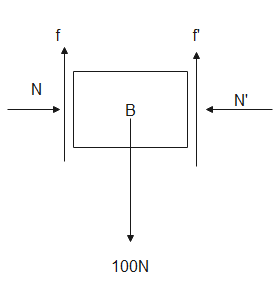
From the above figure, we can see that,
f−f′=100N⇒30−f′=100N⇒f′=30−100∴f′=−70N
Here, f′ is frictional force acting between block B and wall
The negative sign indicates that the direction of f′ assumed for the sake of solving is opposite to its original direction.
Therefore, the frictional force acting between the wall and block B is 70N.
Hence the correct option is (B).
Note:
The normal force as well as the frictional force follows Newton’s third law which states that the forces are equal and opposite in nature. The normal reaction is perpendicular to the surfaces. The force of gravity passes through the centre of mass. The system of blocks was not isolated as an external force was pressing them to the wall.
