Question

Given f(x) is a polynomial function of x, f(x) ⋅ f(y) = f(x) + f(y) + f(xy) - 2 for all x, y ∈ R and that f(2) = 5 Then f(3) is equal to

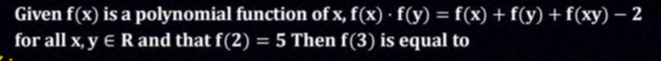
• A. 10
• B. 5
• C. 7
• D. 2

Answer 1

Answer: (A)

10

Answer 2

The given functional equation is: $f(x) \cdot f(y) = f(x) + f(y) + f(xy) - 2$ for all $x, y \in \mathbb{R}$. We are also given that $f(x)$ is a polynomial function and $f(2) = 5$.

Rearranging the functional equation: $f(x) \cdot f(y) - f(x) - f(y) = f(xy) - 2$ Add 1 to both sides to facilitate factorization: $f(x) \cdot f(y) - f(x) - f(y) + 1 = f(xy) - 2 + 1$ $(f(x) - 1)(f(y) - 1) = f(xy) - 1$

Let $g(x) = f(x) - 1$. Since $f(x)$ is a polynomial, $g(x)$ must also be a polynomial. Substituting $g(x)$ into the transformed equation, we get: $g(x) \cdot g(y) = g(xy)$

This is a standard functional equation. We need to find the polynomial solutions for $g(x)$. The polynomial solutions for $g(x)g(y) = g(xy)$ are $g(x) = 0$, $g(x) = 1$, and $g(x) = x^k$ for $k \in \mathbb{Z}^+$.

Case 1: $g(x) = 0$. This implies $f(x) - 1 = 0 \implies f(x) = 1$. If $f(x) = 1$, then $f(2) = 1$, which contradicts $f(2) = 5$.

Case 2: $g(x) = 1$. This implies $f(x) - 1 = 1 \implies f(x) = 2$. If $f(x) = 2$, then $f(2) = 2$, which also contradicts $f(2) = 5$.

Case 3: $g(x) = x^k$ for some positive integer $k$. This means $f(x) - 1 = x^k$, so $f(x) = x^k + 1$. We are given $f(2) = 5$. Substitute $x=2$: $f(2) = 2^k + 1 = 5$ $2^k = 4$ $2^k = 2^2$ Therefore, $k = 2$.

The polynomial function is $f(x) = x^2 + 1$. Now we need to find $f(3)$: $f(3) = 3^2 + 1$ $f(3) = 9 + 1$ $f(3) = 10$.