Question

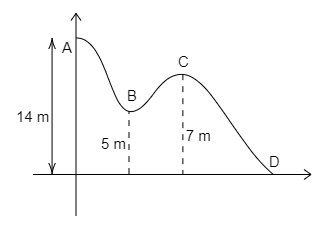
Given figure shows the vertical section of a frictionless surface. A block of mass $2\,kg$ is released from the position $A$, its kinetic energy as it reaches the position $C$ is:

(A) $180\,J$
(B) $140\,J$
(C) $40\,J$
(D) $280\,J$

Answer 1

In this question it is given that the mass of the block is at some height after some time it is released from one position after releasing the block and gets one position. So that the kinetic energy of the required position is equal to the potential energy of the initial position, which is given by the law of conservation of energy.

Useful formula
The law of conservation of energy shows that the energy in a system are equal, then
$KE = PE$
Where, $KE$ is the kinetic energy of the block and $PE$ is the potential energy of the block.
The potential energy of the block is given by,
$PE = mgh$
Where, $PE$ is the potential energy of the block, $m$ is the mass of the block, $g$ is the acceleration due to gravity on the block and $h$ is the height of the block.

Complete step by step solution
Given that,
The mass of the block is, $m = 2\,kg$,
The height of the block at the position of $A$ is, ${h_A} = 14\,m$,
The height of the block at the position of $C$ is, ${h_C} = 7\,m$.
Now,
The law of conservation of energy shows that the energy in a system are equal, then
$KE = PE\,.......................\left( 1 \right)$
The potential energy of the block is given by,
$PE = mgh\,...................\left( 2 \right)$
Now substituting the mass of the block, acceleration of the block due to gravity and the height between the position $A$ and the position $C$ in the above equation (2), then
$PE = 2 \times 10 \times \left( {14 - 7} \right)$
Here, the acceleration due to gravity is taken as $10\,m{s^{ - 2}}$ and the height of the block between the position $A$ and the position $C$, the height value is taken from the graph.
Now subtracting the terms in the above equation, then
$PE = 2 \times 10 \times 7$
By multiplying the terms in the above equation, then
$PE = 140\,J$
By substituting the above equation in the equation (1), then
$KE = PE = 140\,J$
Thus, the above equation shows the kinetic energy as the block reaches the position $C$.

Hence, the option (B) is the correct answer.

Note The energy can neither be created nor destroyed. The energy can be transferred from one form to another form. In this question, the block is kept in some height, so that the block will have the potential energy, when the block is released, the potential energy of the block is changed to the kinetic energy of the block, this statement is given by law of conservation of the energy.