Question

Given f: A→ B.

In the List-I there are some conditions and in the List-Il there are number of functions satisfying the conditions in the List-l. Match List-I with List-Il and select the correct answer using the code given below the list.

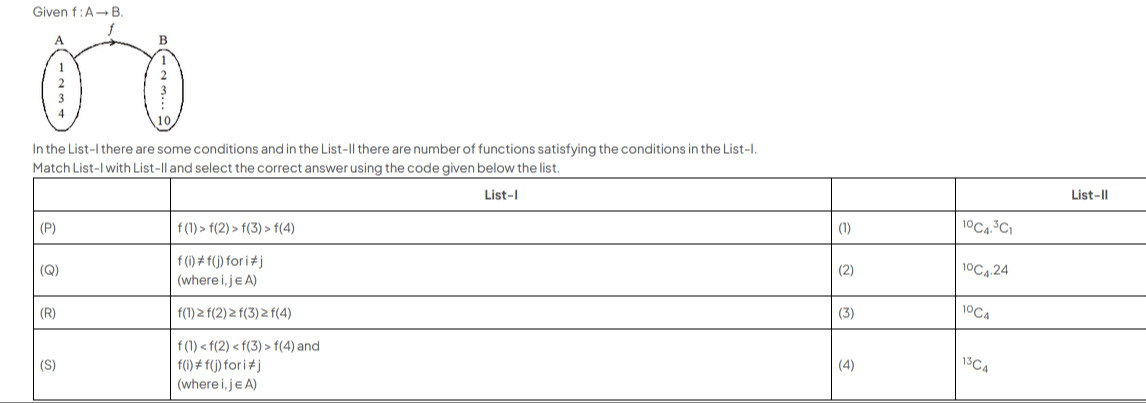
• A. f (1) > f(2) > f(3) > f(4)
• B. f (i)≠f(j) for i≠j (where i, j∈ A)
• C. f(1) ≥ f(2) ≥ f(3) ≥ f(4)
• D. f (1) <f(2) <f(3) > f(4) and f(i)≠f(j) fori #j (where i, j∈ A)

Answer 1

P-3, Q-2, R-4, S-1

Answer 2

The domain is $A = \{1, 2, 3, 4\}$ and the codomain is $B = \{1, 2, \dots, 10\}$.

(P) $f(1) > f(2) > f(3) > f(4)$. This is a strictly decreasing function. To define such a function, we need to choose 4 distinct values from the codomain $B$. Once 4 distinct values are chosen, say $y_1, y_2, y_3, y_4$ with $y_1 > y_2 > y_3 > y_4$, there is only one way to assign them to $f(1), f(2), f(3), f(4)$ to satisfy the condition: $f(1) = y_1, f(2) = y_2, f(3) = y_3, f(4) = y_4$. The number of ways to choose 4 distinct elements from 10 is $^{10}C_4$. So, (P) matches with (3) $^{10}C_4$.

(Q) $f(i) \neq f(j)$ for $i \neq j$ (where $i, j \in A$). This condition means the function is injective (one-to-one). To define an injective function from $A$ to $B$, we need to map each element of $A$ to a distinct element of $B$. We choose 4 distinct elements from $B$ and assign them to the 4 elements of $A$. This is the number of permutations of 10 items taken 4 at a time, which is $^{10}P_4 = \frac{10!}{(10-4)!} = \frac{10!}{6!} = 10 \times 9 \times 8 \times 7 = 5040$. Alternatively, choose 4 elements from $B$ in $^{10}C_4$ ways, and then arrange them in $4!$ ways to assign to $f(1), f(2), f(3), f(4)$. So, the number of injective functions is $^{10}C_4 \times 4! = ^{10}C_4 \times 24$. So, (Q) matches with (2) $^{10}C_4.24$.

(R) $f(1) \geq f(2) \geq f(3) \geq f(4)$. This is a non-increasing function. The number of non-increasing functions from a set of size $k$ to a set of size $n$ is given by the multiset coefficient $\binom{n+k-1}{k}$. Here $k = |A| = 4$ and $n = |B| = 10$. The number of non-increasing functions is $\binom{10+4-1}{4} = \binom{13}{4} = ^{13}C_4$. So, (R) matches with (4) $^{13}C_4$.

(S) $f(1) < f(2) < f(3) > f(4)$ and $f(i) \neq f(j)$ for $i \neq j$. The condition $f(i) \neq f(j)$ for $i \neq j$ means the function is injective. The conditions are $f(1) < f(2) < f(3)$ and $f(3) > f(4)$, with all values distinct. Let $f(1) = a, f(2) = b, f(3) = c, f(4) = d$. We have $a < b < c$ and $c > d$, and $a, b, c, d$ are distinct elements from $\{1, 2, \dots, 10\}$. Consider the possible values for $f(3) = c$. Let $c = k$, where $k \in \{1, 2, \dots, 10\}$. Since $a < b < c$, we must choose $a$ and $b$ from $\{1, 2, \dots, k-1\}$ such that $a < b$. The number of ways to choose 2 distinct values from $k-1$ is $^{k-1}C_2$. Since $c > d$ and $d \neq a, d \neq b$, we must choose $d$ from $\{1, 2, \dots, k-1\} \setminus \{a, b\}$ or from $\{k+1, \dots, 10\}$. Since $a, b, c, d$ must be distinct, $d$ must be chosen from $B \setminus \{a, b, c\}$. The size of this set is $10 - 3 = 7$. Also, $d < c$. So $d$ must be chosen from $\{1, 2, \dots, c-1\}$. The elements $a, b$ are chosen from $\{1, 2, \dots, c-1\}$. So $d$ must be chosen from $\{1, 2, \dots, c-1\} \setminus \{a, b\}$. The size of $\{1, 2, \dots, c-1\}$ is $c-1$. Since $a, b$ are distinct elements from this set, there are $c-1-2 = c-3$ choices for $d$ from this set. However, $d$ can also be greater than $c$. The condition is $c > d$. So $d$ must be chosen from $\{1, 2, \dots, c-1\}$. The set of possible values for $a, b, d$ is $\{1, 2, \dots, c-1\}$. We need to choose 3 distinct values from this set and assign them to $a, b, d$. Once we choose 3 distinct values from $\{1, 2, \dots, c-1\}$, say $v_1 < v_2 < v_3$, we must have $a = v_1$, $b = v_2$, and $d$ can be any of the 3 chosen values. But the conditions are $a < b < c$ and $d < c$. Let's consider choosing 4 distinct values from $B$. Let the chosen values be $x_1 < x_2 < x_3 < x_4$. We need to assign these values to $f(1), f(2), f(3), f(4)$ such that $f(1) < f(2) < f(3) > f(4)$. Let $f(3) = x_i$ for some $i$. If $f(3) = x_1$, then $f(1) < f(2) < x_1$. This is impossible since $x_1$ is the smallest. If $f(3) = x_2$, then $f(1) < f(2) < x_2$. This means $f(1), f(2)$ must be chosen from $\{x_1\}$, which is impossible as they must be distinct. If $f(3) = x_3$, then $f(1) < f(2) < x_3$ and $x_3 > f(4)$. We need to choose $f(1), f(2)$ from $\{x_1, x_2\}$ such that $f(1) < f(2)$. This means $f(1) = x_1, f(2) = x_2$. We need to choose $f(4)$ from $\{x_1, x_2, x_4\}$ such that $f(4) < x_3$. So $f(4)$ can be $x_1$ or $x_2$. But $f(i)$ must be distinct. If $f(4) = x_1$, then $f(1) = x_1$, which is not allowed. If $f(4) = x_2$, then $f(2) = x_2$, which is not allowed. So $f(3)$ cannot be $x_3$.

Let's rephrase the condition. We need to choose 4 distinct values from $B$. Let the set of these 4 values be $S = \{v_1, v_2, v_3, v_4\}$ where $v_1 < v_2 < v_3 < v_4$. We need to assign these values to $f(1), f(2), f(3), f(4)$ such that $f(1) < f(2) < f(3)$ and $f(3) > f(4)$. Let $f(3) = v_i$. If $f(3) = v_1$, impossible as $f(1) < f(2) < v_1$. If $f(3) = v_2$, then $f(1), f(2)$ must be chosen from $\{v_1\}$ such that $f(1) < f(2)$, impossible. If $f(3) = v_3$, then $f(1), f(2)$ must be chosen from $\{v_1, v_2\}$ such that $f(1) < f(2)$. So $f(1) = v_1, f(2) = v_2$. Also $v_3 > f(4)$, and $f(4) \in S \setminus \{v_1, v_2, v_3\} = \{v_4\}$. So $f(4) = v_4$. But we need $v_3 > v_4$, which is false since $v_3 < v_4$. So $f(3)$ cannot be $v_3$. If $f(3) = v_4$, then $f(1), f(2)$ must be chosen from $\{v_1, v_2, v_3\}$ such that $f(1) < f(2)$. There are $^{3}C_2 = 3$ ways to choose $\{f(1), f(2)\}$, and once chosen, $f(1)$ and $f(2)$ are determined. So $(f(1), f(2))$ can be $(v_1, v_2), (v_1, v_3), (v_2, v_3)$. Also $v_4 > f(4)$, and $f(4) \in \{v_1, v_2, v_3\}$. The value of $f(4)$ must be the remaining value in $\{v_1, v_2, v_3\}$ that is not assigned to $f(1)$ or $f(2)$. Let the chosen set of 4 values be $S = \{v_1, v_2, v_3, v_4\}$. We assign $v_4$ to $f(3)$. We need to assign $v_1, v_2, v_3$ to $f(1), f(2), f(4)$ such that $f(1) < f(2)$ and $f(4) < v_4$. We choose 2 elements from $\{v_1, v_2, v_3\}$ for $f(1)$ and $f(2)$ such that $f(1) < f(2)$. This can be done in $^{3}C_2 = 3$ ways. The remaining element is assigned to $f(4)$. Since the remaining element is from $\{v_1, v_2, v_3\}$, it is less than $v_4$. So the condition $f(4) < v_4$ is satisfied. The possible assignments are:

1. $\{f(1), f(2)\} = \{v_1, v_2\}$. Then $f(1) = v_1, f(2) = v_2$. The remaining element is $v_3$. So $f(4) = v_3$. We have $v_1 < v_2 < v_4$ and $v_4 > v_3$. This satisfies the condition.
2. $\{f(1), f(2)\} = \{v_1, v_3\}$. Then $f(1) = v_1, f(2) = v_3$. The remaining element is $v_2$. So $f(4) = v_2$. We have $v_1 < v_3 < v_4$ and $v_4 > v_2$. This satisfies the condition.
3. $\{f(1), f(2)\} = \{v_2, v_3\}$. Then $f(1) = v_2, f(2) = v_3$. The remaining element is $v_1$. So $f(4) = v_1$. We have $v_2 < v_3 < v_4$ and $v_4 > v_1$. This satisfies the condition. So for each set of 4 distinct values chosen from $B$, there are 3 ways to assign them to $f(1), f(2), f(3), f(4)$ such that the conditions are met. The number of ways to choose 4 distinct values from 10 is $^{10}C_4$. For each choice, there are 3 valid assignments. So the total number of such functions is $^{10}C_4 \times 3$. $^{10}C_4 = \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} = 10 \times 3 \times 7 = 210$. Number of functions = $210 \times 3 = 630$. Let's check the options in List-II. (1) $^{10}C_4.^3C_1 = 210 \times 3 = 630$. So, (S) matches with (1) $^{10}C_4.^3C_1$.

Summary of matches: (P) - (3) $^{10}C_4$ (Q) - (2) $^{10}C_4.24$ (R) - (4) $^{13}C_4$ (S) - (1) $^{10}C_4.^3C_1$