Question

Given $\Delta ABC$ right angled at C in which AB = 29 units, BC = 21 units and $\angle ABC=\theta$. Find ${{\cos }^{2}}\theta -{{\sin }^{2}}\theta$.

Answer 1

Hint:Given two sides of the right angled triangle. Find the ${{3}^{rd}}$ side, by using basic geometry. Find the value of $\sin \theta$ and $\cos \theta$ from the figure. Substitute these values in ${{\cos }^{2}}\theta -{{\sin }^{2}}\theta$ and get the value.

Complete step-by-step answer:
Consider the figure drawn,

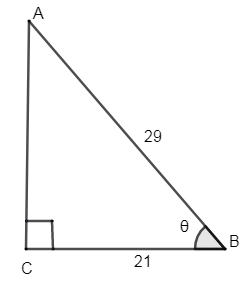
From, $\vartriangle ABC$, AB = 29 units and BC = 21 units, $\angle ABC=\theta$.
Using Pythagoras theorem,

& {{\left( Hypotenuse \right)}^{2}}={{\left( Height \right)}^{2}}+{{\left( Base \right)}^{2}} \\\ & \Rightarrow A{{B}^{2}}=A{{C}^{2}}+A{{B}^{2}} \\\ & A{{C}^{2}}=A{{B}^{2}}-B{{C}^{2}} \\\ & A{{C}^{2}}={{\left( 29 \right)}^{2}}-{{\left( 21 \right)}^{2}} \\\ \end{aligned}$$ Using, $${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$$ $$\begin{aligned} & A{{C}^{2}}=\left( 29-21 \right)\left( 29+21 \right) \\\ & A{{C}^{2}}=8\times 50=400 \\\ & \therefore AC=\sqrt{400}=20 \\\ \end{aligned}$$ Now, $$\sin \theta $$= $$\dfrac{Opposite side}{Hypotenuse side}$$. $$\sin \theta =\dfrac{AC}{AB}=\dfrac{20}{29}$$ $$\cos \theta $$= $$\dfrac{Adjacent side}{Hypotenuse side}$$. $$\cos \theta =\dfrac{BC}{AB}=\dfrac{21}{29}$$ We need to find the value of $${{\cos }^{2}}\theta -{{\sin }^{2}}\theta $$. Putting values of $$\cos \theta =\dfrac{21}{29}$$ and $$\sin \theta =\dfrac{20}{29}$$. $$\begin{aligned} & {{\cos }^{2}}\theta -{{\sin }^{2}}\theta ={{\left( \dfrac{21}{29} \right)}^{2}}-{{\left( \dfrac{20}{29} \right)}^{2}}=\dfrac{{{21}^{2}}-{{20}^{2}}}{{{29}^{2}}} \\\ & \because {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right) \\\ & \Rightarrow \dfrac{\left( 21-20 \right)\left( 21+20 \right)}{{{29}^{2}}}=\dfrac{1\times 41}{{{29}^{2}}}=\dfrac{41}{841} \\\ & \therefore {{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\dfrac{41}{841} \\\ \end{aligned}$$ Note: Find altitude of the $$\Delta ABC$$, which will give the values of $$\cos \theta $$ and $$\sin \theta $$. Put the values in the entity to find the desired answer.Students should remember pythagoras theorem , trigonometric identities and trigonometric ratios for solving these types of problems.