Question

Given, $\cos \alpha = \dfrac{1}{3}$ how do you find $\sin \alpha$ ?

Answer 1

Here we have to find out the value of $\sin \alpha$ . By using the formula and more importantly we use the Pythagoras theorem. After we have done some simplification we get the required answer.

Formula used: Let's say, $ABC$ is a right angled triangle and we want to find the value of Sine and Cosine of the angle $\theta$ mentioned in the picture.

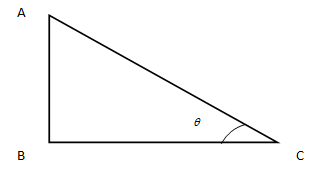
So, according to the property of the right angled triangle, $AB$ is perpendicular, $BC$ is the base and $AC$ is the hypotenuse.
According to Pythagoras theorem:
${{\text{(Perpendicular)}}^{\text{2}}}{\text{ + (Base}}{{\text{)}}^{\text{2}}}{\text{ = (Hypotenuse}}{{\text{)}}^{\text{2}}}$ .
Also, we know that $\sin \theta$ is the ratio of the perpendicular and hypotenuse.
And, $\cos \theta$ is the ratio of the base and hypotenuse.
So, we can rewrite as in the following form using the above triangle:
$\sin \theta = \dfrac{{AB}}{{AC}}$ and $\cos \theta = \dfrac{{BC}}{{AC}}$ .

Complete step-by-step solution:
It is given in the question that:
$\operatorname{Cos} \alpha = \dfrac{1}{3}$ .
So, according to above formula,
${{cos\alpha = }}\dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{3}}}$ .
Let say, ${\text{Base = x}}$ and ${\text{Hypotenuse = 3x}}$ .
So, we can draw the following triangle:

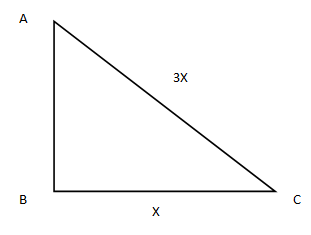
So, we can use Pythagoras theorem to find the value of $AB$ .
So, we can write it as following:
$\Rightarrow A{B^2} + B{C^2} = A{C^2}$ .
Now, put the value of $BC = x$ and $AC = 3x$ in the above equation, we get:
$\Rightarrow A{B^2} + {\left( x \right)^2} = {\left( {3x} \right)^2}$ .
So, by doing squared the terms, we get:
$\Rightarrow A{B^2} + {x^2} = 9{x^2}$ .
Now, take the variables to the L.H.S, we get:
$\Rightarrow A{B^2} = 9{x^2} - {x^2}$ .
Now, doing further simplification, we get:
$\Rightarrow A{B^2} = 8{x^2}$ .
Now, taking the square root on both the sides, we get:
$\Rightarrow AB = \sqrt {8{x^2}} = 2\sqrt 2 x$ .
Now, we know that $\sin \theta$ is the ratio of the perpendicular and hypotenuse.
So, ${{sin\alpha = }}\dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{AC}}}}{\text{ = }}\dfrac{{{\text{2}}\sqrt {\text{2}} {\text{x}}}}{{{\text{3x}}}}{\text{ = }}\dfrac{{{\text{2}}\sqrt {\text{2}} }}{{\text{3}}}{\text{.}}$

Therefore, the value of $\sin \alpha$ is $\dfrac{{2\sqrt 2 }}{3}$ .

Note: Alternative solution:
We can use another formula directly to solve this question.
We can use ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$ formula to solve this question.
Here it is given that: $\cos \alpha = \dfrac{1}{3}$ .
By putting this value into the above equation, we get: ${\sin ^2}\alpha + {\left( {\dfrac{1}{3}} \right)^2} = 1$ .
Now, by solving it, we get:
${\sin ^2}\alpha = 1 - \dfrac{1}{9}$
$\Rightarrow {\sin ^2}\alpha = \dfrac{8}{9}$
$\Rightarrow \sin \alpha = \pm \sqrt {\dfrac{8}{9}}$
$\Rightarrow \sin \alpha = \pm \dfrac{{2\sqrt 2 }}{3}$
Negative sign indicates the negative coordinates.