Question

Given $ABCD$ is a rectangle with $B\left( -5,0 \right),C\left( 7,0 \right)$ and $D\left( 7,3 \right)$ . What is the coordinate of $A$ ?

Answer 1

Here we have been given a rectangle whose three points are given and we have to find the coordinate of its fourth point. We will use the coordinate of the midpoint of the two diagonals of the rectangle for finding the coordinate of the fourth point. We will set the coordinate of the fourth point as $\left( x,y \right)$ then by using the midpoint formula we will find the midpoint of $BD$ and $AC$ . Finally by comparing the two values we will get the desired answer.

Complete step by step answer:
The rectangle is given as $ABCD$ and the three points of it is given as follows:
$B\left( -5,0 \right),C\left( 7,0 \right)$ and $D\left( 7,3 \right)$
Let the fourth point coordinate be $A\left( x,y \right)$.
So we can draw the rectangle as follows:

Now as we can see that the diagonal of above rectangle is $BD$ and $AC$ drawn as follows:

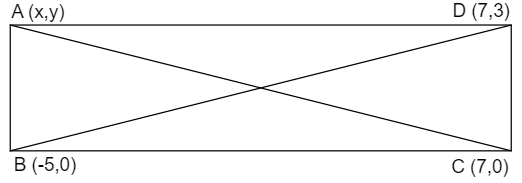
We know that both the diagonal intersect at the middle point so we will find the midpoint of the two diagonal by using the formula below:
$\left( a,b \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$…$\left( 1 \right)$
Where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$are the coordinate of the two points and $\left( a,b \right)$ is the coordinate of the midpoint.
So we want to find the midpoint of $BC$ and we have,
$B=\left( -5,0 \right)$ and $D=\left( 7,3 \right)$
So using formula (1) we get,
$\left( a,b \right)=\left( \dfrac{-5+7}{2},\dfrac{0+3}{2} \right)$
$\Rightarrow \left( a,b \right)=\left( \dfrac{2}{2},\dfrac{3}{2} \right)$
So we get,
$\left( a,b \right)=\left( 1,\dfrac{3}{2} \right)$….$\left( 2 \right)$
Next we want to find the midpoint of $AC$ and we have,
$A=\left( x,y \right)$ and $C=\left( 7,0 \right)$
So using formula (1) we get,
$\left( c,d \right)=\left( \dfrac{x+7}{2},\dfrac{y+0}{2} \right)$
$\Rightarrow \left( c,d \right)=\left( \dfrac{x+7}{2},\dfrac{y}{2} \right)$….$\left( 3 \right)$
As we know that the diagonal bisect each other so the point in equation (2) and (3) will be equal so,
$\dfrac{x+7}{2}=1$ And $\dfrac{y}{2}=\dfrac{3}{2}$
On solving we get,
$\Rightarrow \dfrac{x+7}{2}=1$
$\Rightarrow x+7=2$
So,
$\Rightarrow x=2-7$
$\Rightarrow x=-5$
Next we have,
$\Rightarrow \dfrac{y}{2}=\dfrac{3}{2}$
$\Rightarrow y=\dfrac{3}{2}\times 2$
So we get,
$\Rightarrow y=3$
So we got $x=-5,y=3$.
Therefore $A=\left( -5,3 \right)$
The rectangle can be drawn as:

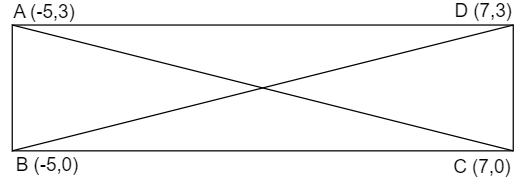
Hence in rectangle $ABCD$ with $B\left( -5,0 \right),C\left( 7,0 \right)$ and $D\left( 7,3 \right)$ the coordinate of $A=\left( -5,3 \right)$ .

Note:
In this type of question, always try to find the relation between the unknown point and the points given. This question can also be solved by the property of a rectangle as we can draw the rectangle on a graph by plotting the point given and as the opposite sides of the rectangle are of equal length and we can find length using distance formula and we can get our fourth coordinate.