Question
Question: Given $a,b \in\{0, 1, 2, 3, 4, \dots, 9, 10\}$. Consider the system of equations $x+y+z=4$ $2x+y+3z...
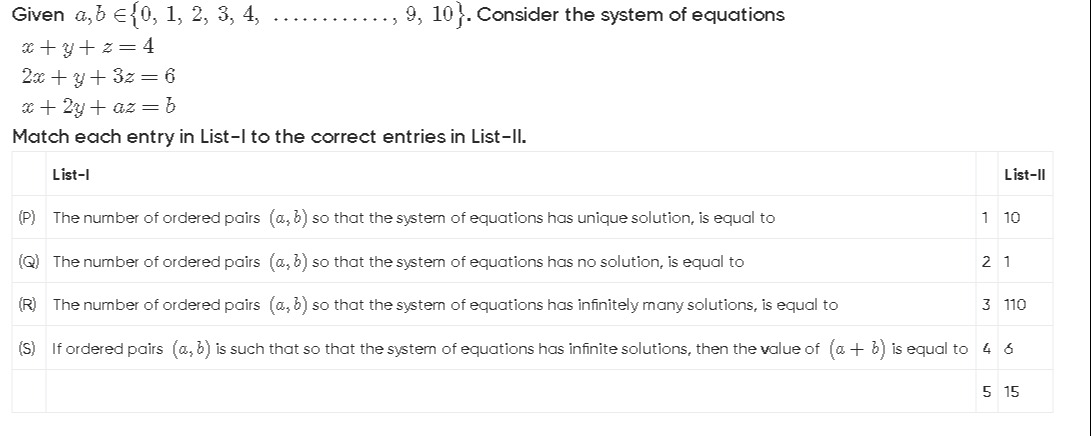
Given a,b∈{0,1,2,3,4,…,9,10}. Consider the system of equations
x+y+z=4 2x+y+3z=6 x+2y+az=b
Match each entry in List-I to the correct entries in List-II.
| List-I | List-II | ||
|---|---|---|---|
| (P) | The number of ordered pairs (a,b) so that the system of equations has unique solution, is equal to | 1 | 10 |
| (Q) | The number of ordered pairs (a,b) so that the system of equations has no solution, is equal to | 2 | 1 |
| (R) | The number of ordered pairs (a,b) so that the system of equations has infinitely many solutions, is equal to | 3 | 110 |
| (S) | If ordered pairs (a,b) is such that so that the system of equations has infinite solutions, then the value of (a+b) is equal to | 4 | 6 |
| 5 | 15 |
P → 3; Q → 1; R → 2; S → 4
Solution
The given system of linear equations is:
- x+y+z=4
- 2x+y+3z=6
- x+2y+az=b
The parameters a,b∈{0,1,2,…,10}. There are 11 possible values for a and 11 possible values for b.
We can analyze the system using the determinant of the coefficient matrix or by Gaussian elimination. Let's use Gaussian elimination. The augmented matrix for the system is: M=12111213a∣∣∣46b
Perform row operations to simplify the matrix: R2→R2−2R1: 1011−1211a∣∣∣4−2b
R3→R3−R1: 1001−1111a−1∣∣∣4−2b−4
R2→−R2: 1001111−1a−1∣∣∣42b−4
R3→R3−R2: 1001101−1(a−1)−(−1)∣∣∣42(b−4)−2 1001101−1a∣∣∣42b−6
Now we analyze the system based on the last row, which corresponds to the equation az=b−6.
1. Unique Solution (P): A system has a unique solution if the determinant of the coefficient matrix is non-zero. From the row-echelon form, this means the coefficient of z in the last equation must be non-zero. So, a=0. Since a∈{0,1,…,10}, the possible values for a are {1,2,…,10}, which is 10 choices. The value of b does not affect the existence of a unique solution when a=0. So, b∈{0,1,…,10}, which is 11 choices. The number of ordered pairs (a,b) for which the system has a unique solution is 10×11=110. This matches with List-II entry 3. So, P → 3.
2. No Solution (Q): A system has no solution if it leads to a contradiction. In our simplified form, this occurs when a=0 and b−6=0. So, a=0 (1 choice). And b−6=0⟹b=6. Since b∈{0,1,…,10}, the possible values for b are {0,1,2,3,4,5,7,8,9,10}, which is 10 choices. The number of ordered pairs (a,b) for which the system has no solution is 1×10=10. This matches with List-II entry 1. So, Q → 1.
3. Infinitely Many Solutions (R): A system has infinitely many solutions if it is consistent and has at least one free variable. In our simplified form, this occurs when a=0 and b−6=0. So, a=0 (1 choice). And b−6=0⟹b=6 (1 choice). The number of ordered pairs (a,b) for which the system has infinitely many solutions is 1×1=1. This ordered pair is (0,6). This matches with List-II entry 2. So, R → 2.
4. Value of (a+b) for infinite solutions (S): From the analysis for infinitely many solutions, the only ordered pair (a,b) that yields infinite solutions is (0,6). For this pair, a+b=0+6=6. This matches with List-II entry 4. So, S → 4.
Summary of Matches:
- (P) → 3
- (Q) → 1
- (R) → 2
- (S) → 4
The final answer is P→3;Q→1;R→2;S→4.
