Question

Given, $A^{2+}(aq) + 2e^{-} \rightleftharpoons A(s) \quad E^{\circ} = -0.96 V$

$ACl_2(s) + 2e^{-} \rightleftharpoons A(s) + 2Cl^-(aq) \quad E^{\circ} = -1.1V$

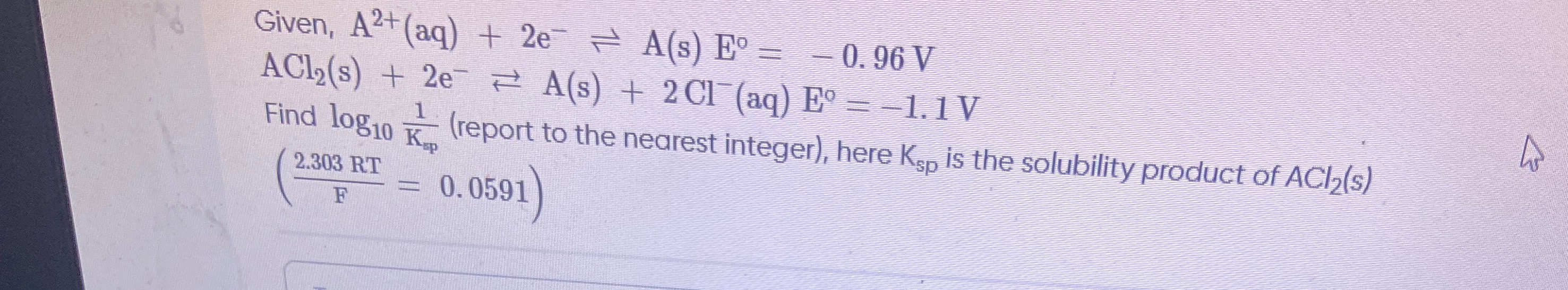
Find $\log_{10} \frac{1}{K_{sp}}$ (report to the nearest integer), here $K_{sp}$ is the solubility product of $ACl_2(s)$ $\left(\frac{2.303 RT}{F} = 0.0591\right)$

Answer 1

5

Answer 2

To find the solubility product constant ($K_{sp}$) for $ACl_2(s)$, we need to relate the given standard electrode potentials to the dissolution reaction of $ACl_2$.

The dissolution reaction for $ACl_2(s)$ is: $ACl_2(s) \rightleftharpoons A^{2+}(aq) + 2Cl^-(aq)$

We are given the following standard electrode potentials:

1. $A^{2+}(aq) + 2e^{-} \rightleftharpoons A(s) \quad E^{\circ}_1 = -0.96 V$
2. $ACl_2(s) + 2e^{-} \rightleftharpoons A(s) + 2Cl^-(aq) \quad E^{\circ}_2 = -1.1V$

To obtain the dissolution reaction, we can subtract the first half-reaction from the second half-reaction: $(ACl_2(s) + 2e^{-} \rightleftharpoons A(s) + 2Cl^-(aq))$ $- (A^{2+}(aq) + 2e^{-} \rightleftharpoons A(s))$

---

$ACl_2(s) - A^{2+}(aq) \rightleftharpoons 2Cl^-(aq)$

Rearranging this gives the dissolution reaction: $ACl_2(s) \rightleftharpoons A^{2+}(aq) + 2Cl^-(aq)$

The standard cell potential ($E^\circ_{cell}$) for this reaction is the difference between the standard electrode potentials: $E^\circ_{cell} = E^\circ_2 - E^\circ_1$ $E^\circ_{cell} = (-1.1 V) - (-0.96 V)$ $E^\circ_{cell} = -1.1 V + 0.96 V$ $E^\circ_{cell} = -0.14 V$

This $E^\circ_{cell}$ is related to the equilibrium constant ($K_{sp}$ in this case) by the Nernst equation at standard conditions: $E^\circ_{cell} = \frac{2.303 RT}{nF} \log_{10} K_{sp}$

We are given $\left(\frac{2.303 RT}{F} = 0.0591\right)$. In the dissolution reaction $ACl_2(s) \rightleftharpoons A^{2+}(aq) + 2Cl^-(aq)$, the number of electrons transferred ($n$) is 2 (as derived from the half-reactions).

Substitute the values into the equation: $-0.14 V = \frac{0.0591 V}{2} \log_{10} K_{sp}$ $-0.14 = 0.02955 \log_{10} K_{sp}$

Now, solve for $\log_{10} K_{sp}$: $\log_{10} K_{sp} = \frac{-0.14}{0.02955}$ $\log_{10} K_{sp} \approx -4.7377$

The question asks for $\log_{10} \frac{1}{K_{sp}}$. $\log_{10} \frac{1}{K_{sp}} = -\log_{10} K_{sp}$ $\log_{10} \frac{1}{K_{sp}} = -(-4.7377)$ $\log_{10} \frac{1}{K_{sp}} = 4.7377$

Rounding to the nearest integer, $4.7377$ is approximately 5.