Question
Question: Given a first order reaction which takes place as follows: $A(g) \rightarrow 2B(g) + C(g)$ Total p...
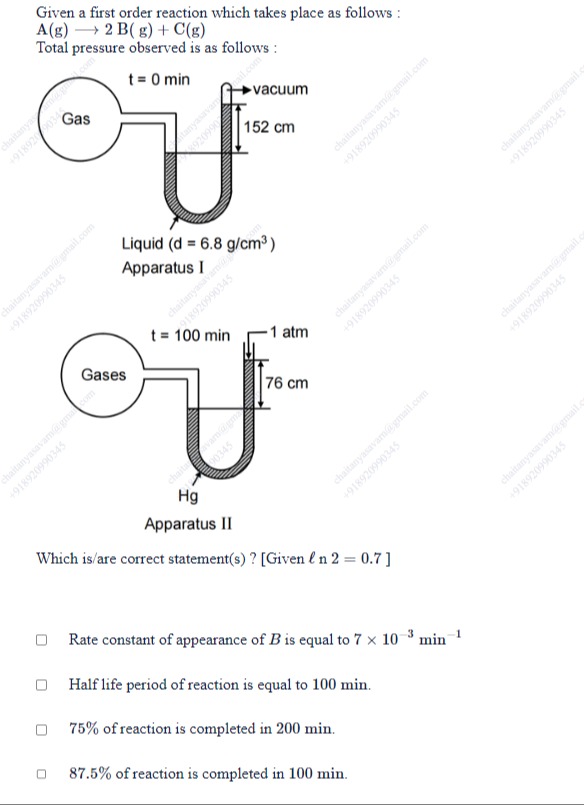
Given a first order reaction which takes place as follows:
A(g)→2B(g)+C(g)
Total pressure observed is as follows:
Which is/are correct statement(s)? [Given ln2=0.7]
Rate constant of appearance of B is equal to 7×10−3min−1
Half life period of reaction is equal to 100 min.
75% of reaction is completed in 200 min.
87.5% of reaction is completed in 100 min.
Rate constant of appearance of B is equal to 7×10−3min−1, Half life period of reaction is equal to 100 min., 75% of reaction is completed in 200 min.
Solution
We start with the reaction
A(g)→2B(g)+C(g)
Let the initial number of moles of A be 1. If a fraction x has reacted at time t, then:
- Moles of unreacted A: 1−x
- Moles of products: 3x (since 1 mole of A gives 2 moles of B and 1 mole of C)
- Total moles at time t: (1−x)+3x=1+2x
Since the reaction occurs in a closed container at constant temperature and volume, pressure is proportional to the number of moles.
Determining the Pressures
-
At t=0 (Apparatus I):
The manometer uses a liquid with density d=6.8g/cm3. A column of 152cm of that liquid is equivalent to a column of mercury (density 13.6g/cm3) of height:
hHg=152×13.66.8=152×0.5=76cmSince 76cm Hg corresponds to 1atm, the initial pressure P0 is 1atm.
-
At t=100 min (Apparatus II):
The manometer now uses mercury directly. The 76cm difference when one arm is open to the atmosphere (1 atm) indicates that the gas in the bulb exerts a pressure of:
P=1atm+76cm Hg equivalent=1atm+1atm=2atm.
Relating Pressure to Reaction Progress
Since pressure is proportional to the moles:
P(t)=P0(1+2x)At t=100 min, P=2atm:
2=1(1+2x)⟹1+2x=2⟹x=0.5.So, 50% of the reactant has reacted at 100 min.
For a first order reaction, the fraction reacted is given by:
1−x=e−kt.At x=0.5 (i.e. 50% reacted):
e−k(100)=0.5⟹k=100ln2≈1000.693≈7×10−3min−1.Thus, the half-life t1/2 is 100 min.
Checking the Statements
-
Rate constant of appearance of B is equal to 7×10−3min−1.
Since the reaction is first order, the rate constant calculated is k≈7×10−3min−1.
→ Correct.
-
Half life period of reaction is equal to 100 min.
We found t1/2=100 min.
→ Correct.
-
75% of reaction is completed in 200 min.
For t=200 min:
e−k(200)=e−0.693×2=e−1.386≈0.25.So, fraction reacted is 1−0.25=0.75 or 75%.
→ Correct.
-
87.5% of reaction is completed in 100 min.
At t=100 min we already have 50% conversion, not 87.5%.
→ Incorrect.
