Question
Question: Given,A and B are two points on a uniform ring of radius r. The resistance of the ring is R. \[\angl...
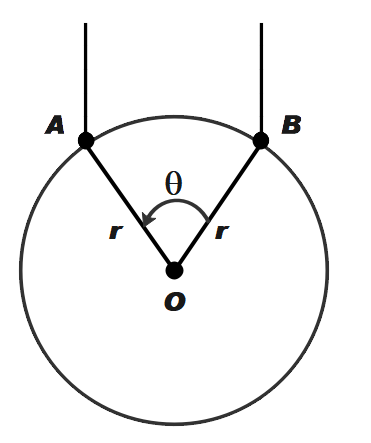
Given,A and B are two points on a uniform ring of radius r. The resistance of the ring is R. ∠AOB=θ as shown in the figure. The equivalent resistance between A and B is:
A. 2πRθ
B. 4πR(2π−θ)
C. R(1−2πθ)
D. 4π2R(2π−θ)θ
Solution
In this question we have been asked to calculate the equivalent resistance between the given points. It is given that A and B are two points on the uniform circular ring. No, from the figure we can say that, the two arcs formed by the points A and B are connected in parallel to each other. Therefore, if we calculate the individual resistance of the bigger and smaller arc, we can calculate the equivalent resistance between points A and B.
Formula used:
l=rθ
Where,
l is the length of the arc,
r is the radius of ring
θ is the angle made by the arc
RAB1=R11+R21
Complete step by step solution:
From the given figure,
We know that the arc length is given by,
l=rθ
Now, calculating the resistance of the smaller arc
We get,
R1=2πrrθR
On solving,
R1=2πθR…………….. (1)
Similarly, for bigger arc
We get,
R2=2π2π−θR …………………… (2)
Now,
From the figure we can say that the two arcs are connected in parallel combination with each other.Therefore, We know,
RAB1=R11+R21
After substituting values from (1) and (2)
We get,
RAB1=θR2π+(2π−θ)R2π
Therefore,
RAB=4π2R(2π−θ)θ
Therefore, the correct answer is option D.
Note:
If two or more resistors in a circuit are connected to the same nodes, the resistors are said to be in parallel connection. The equivalent resistance in parallel connection is given by adding the reciprocals on individual resistance and then taking the reciprocal of the sum. The equivalent resistance is smaller than the resistor with smallest resistance.
